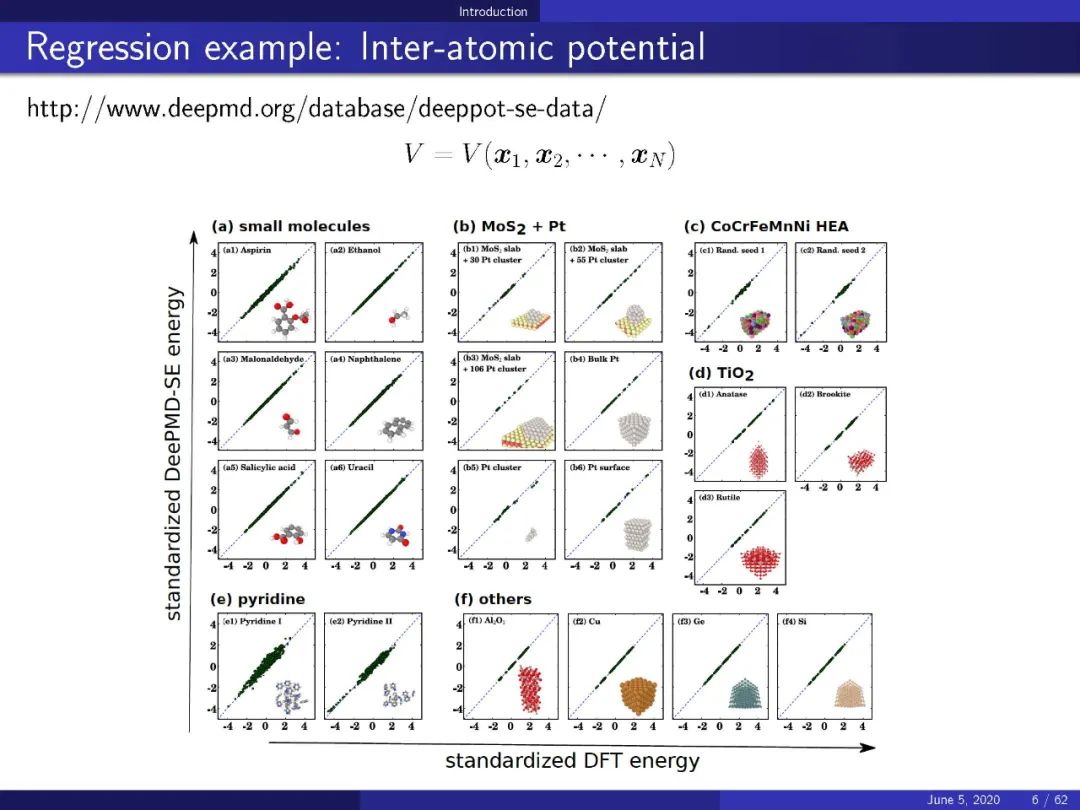
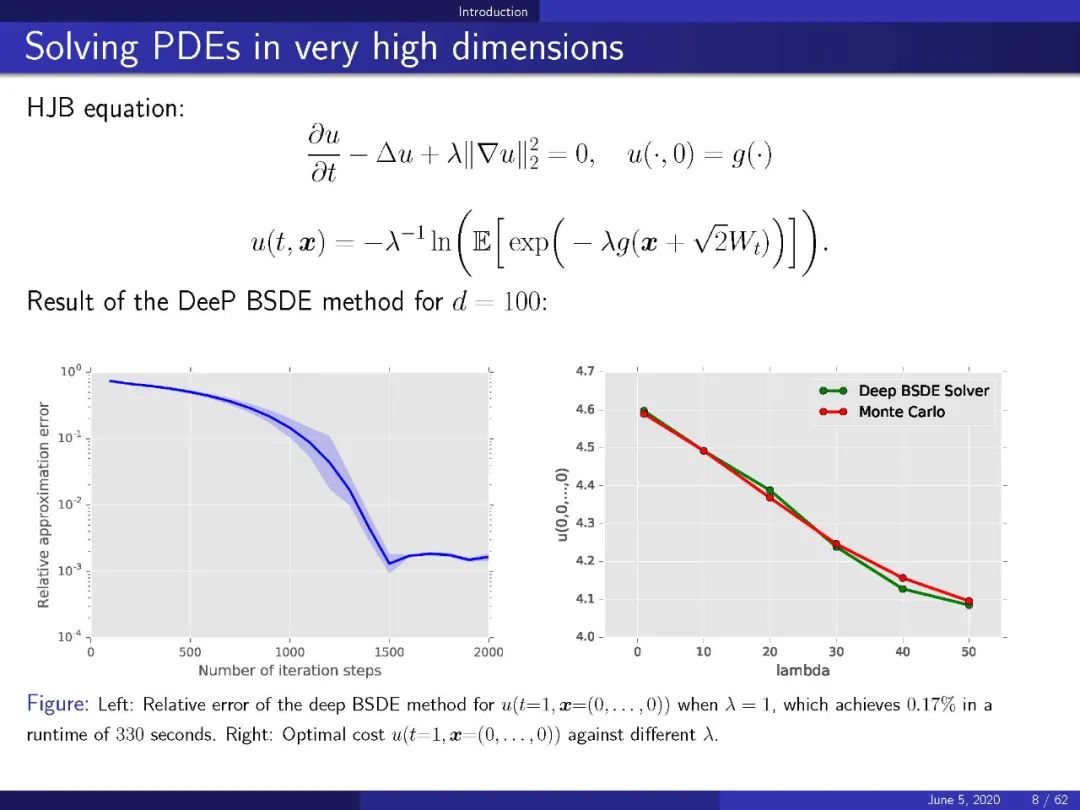
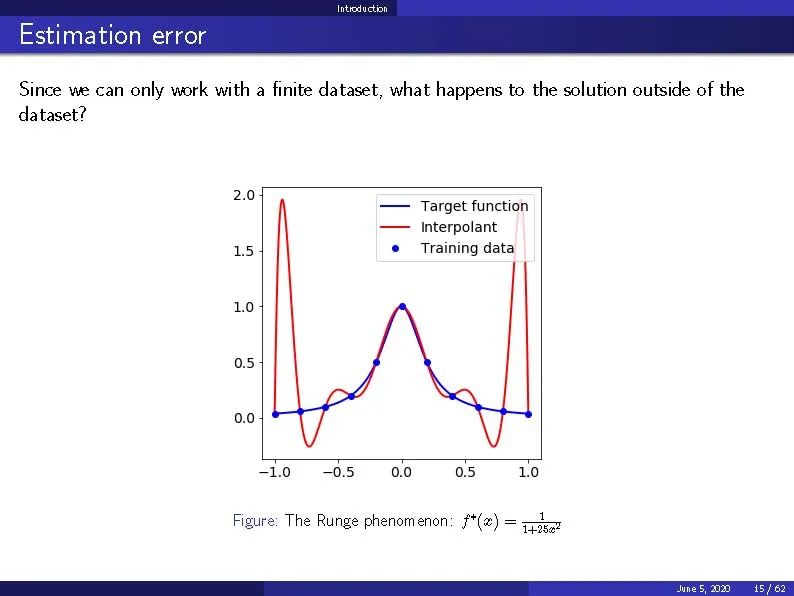
现代机器学习(ML)的核心是高维函数的近似。传统的方法，如用分段多项式、小波或其他固定基函数的线性组合进行逼近，都面临着维数(CoD)的问题。我们将提供ML的数学观点，集中在CoD的问题。我们将讨论三个主要问题: 现代ML模型的近似理论和误差分析，梯度下降算法的动力学和定性行为，以及从连续观点的ML。我们将看到，在连续的水平上，ML可以被表示为一系列合理的漂亮的变分和类似于方程的问题。现代的ML模型/算法，如随机特征模型和两层残差神经网络模型，都可以看作是这类连续问题的特殊离散化。我们还将提供一个适合分析高维ML模型和算法的框架，并提供无CoD的结果。最后，我们将讨论现代ML成功的基本原因，以及仍有待理解的微妙和神秘之处。

https://web.math.princeton.edu/~weinan/

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“ML63” 可以获取《【普林斯顿】机器学习数学视角，63页ppt》专知下载链接索引

专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取5000+AI主题知识资源