https://kexue.fm/archives/5383 

三篇vae写的非常好，个人学习记录如下：

建议直接阅读原文。

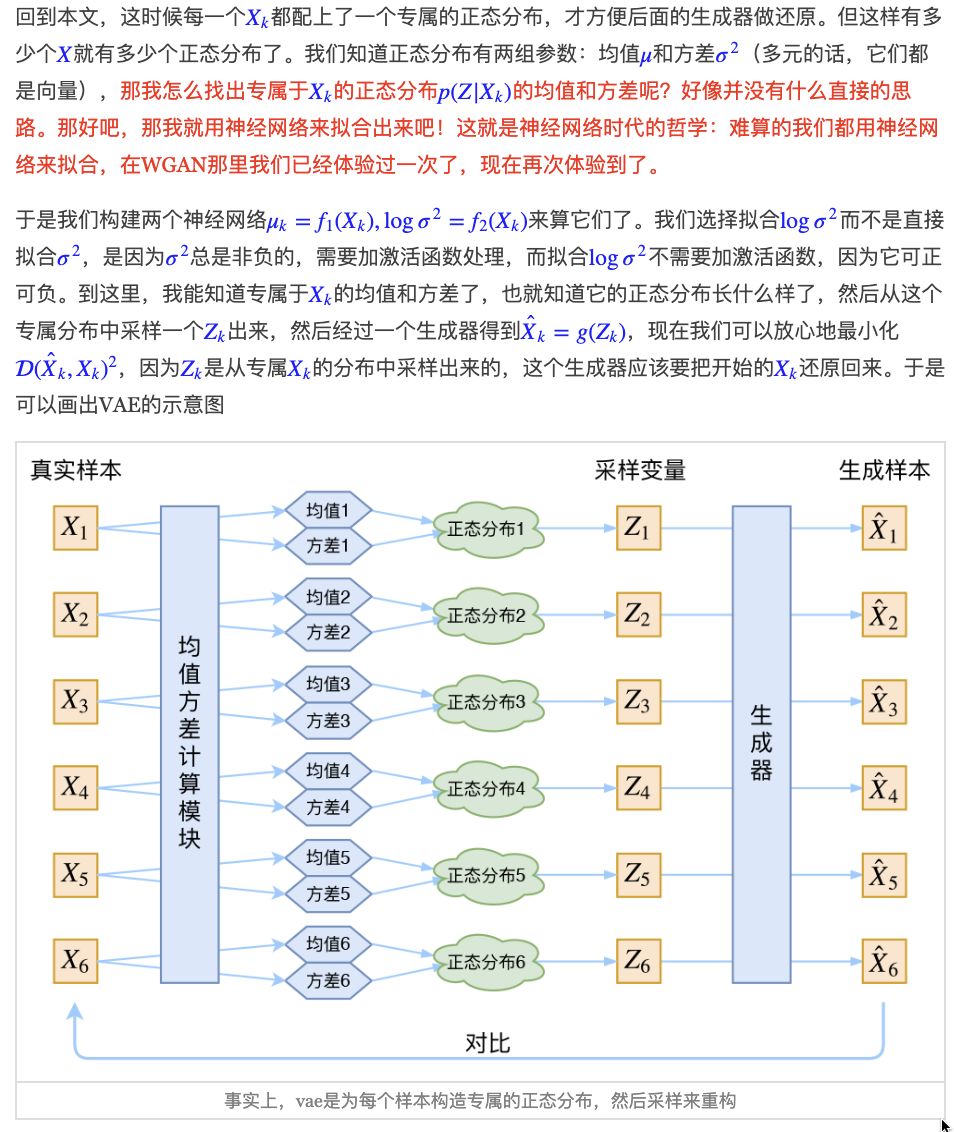
https://kexue.fm/archives/5253  第一篇的截图

通常图片都是有隐变量z 比如100维向量表示。

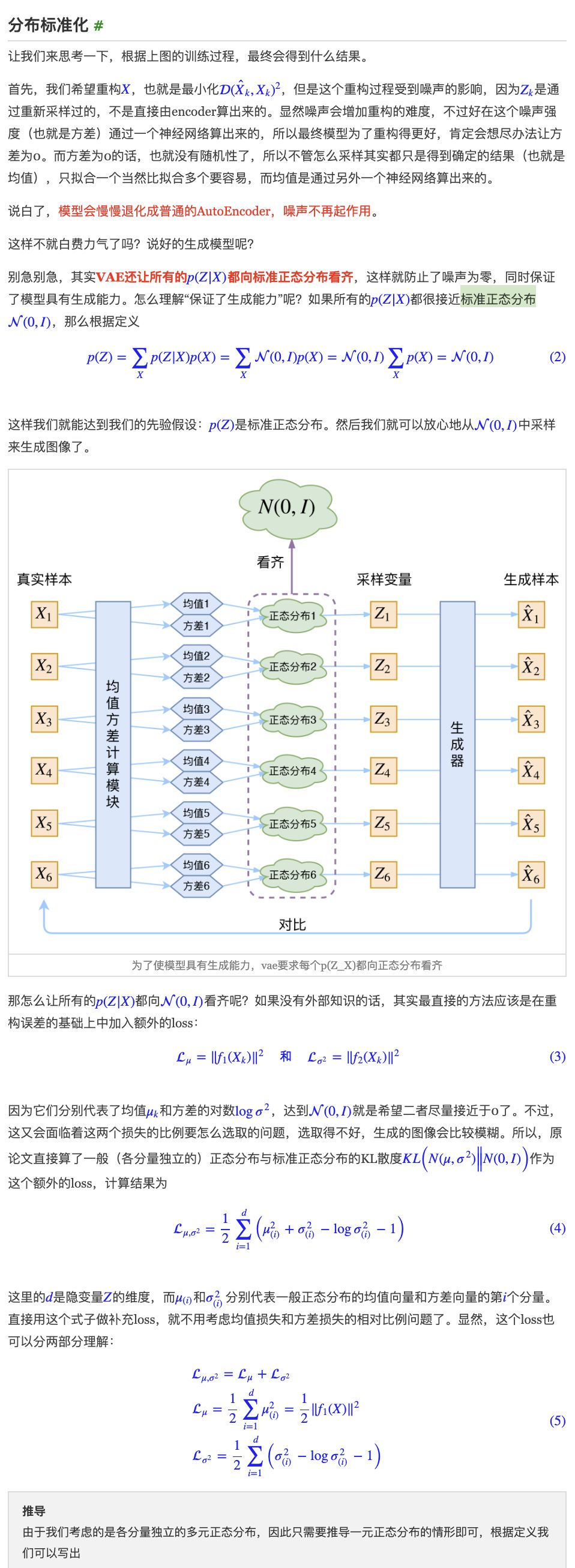
z如果重构的好，那z离正常图片分布就近，离标准正态分布就远，klloss就大。

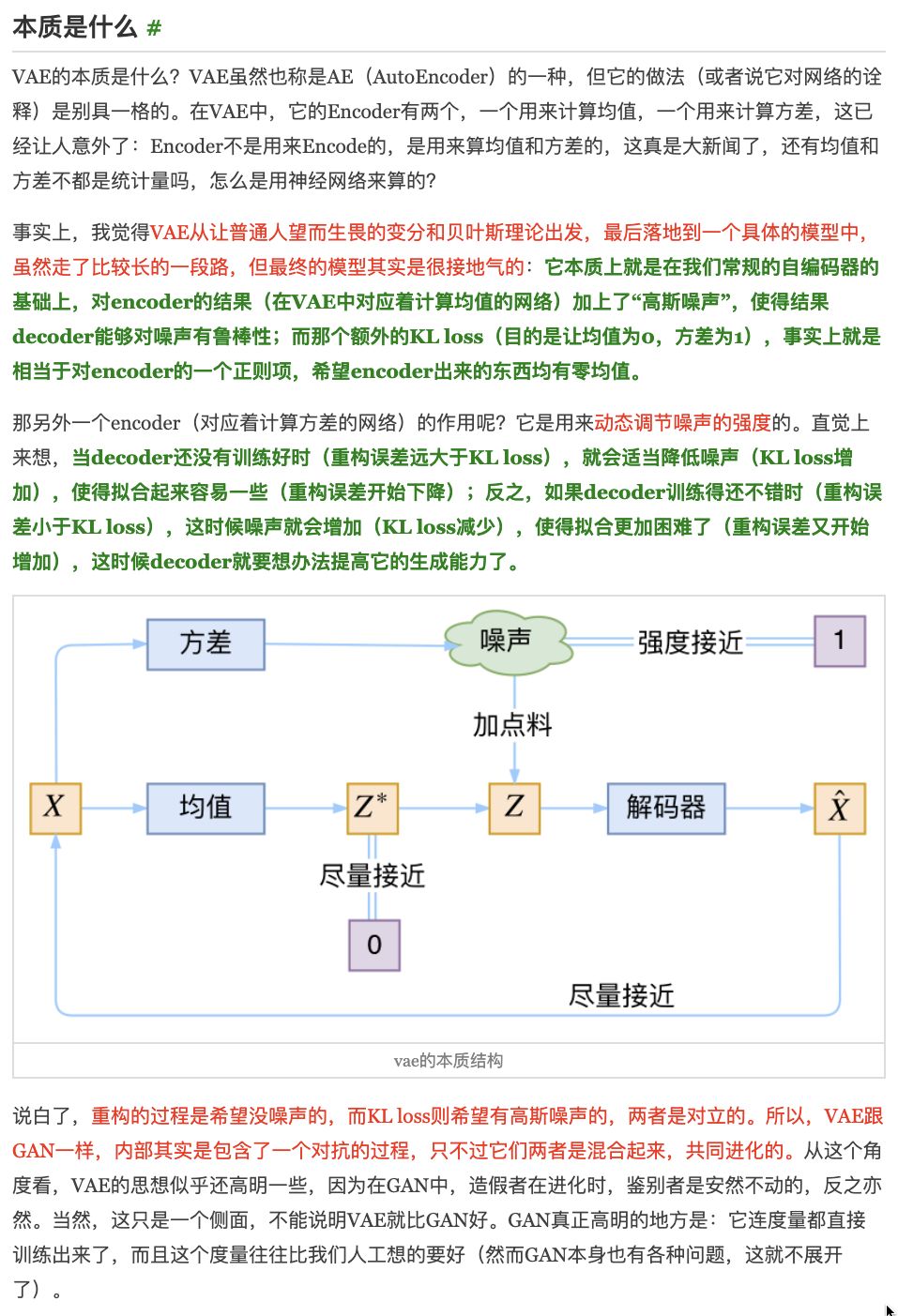
https://kexue.fm/archives/5343  二的截图

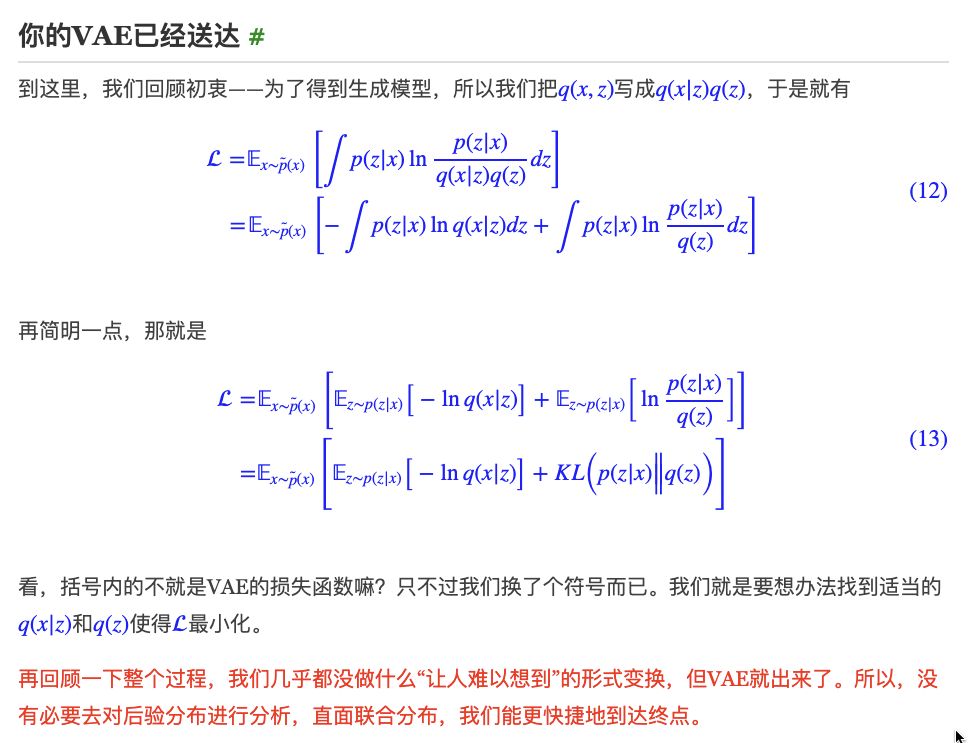
https://kexue.fm/archives/5383  第三篇 

苏剑林. (2018, Apr 03). 《变分自编码器（三）：这样做为什么能成？ 》[Blog post]. Retrieved from https://kexue.fm/archives/5383