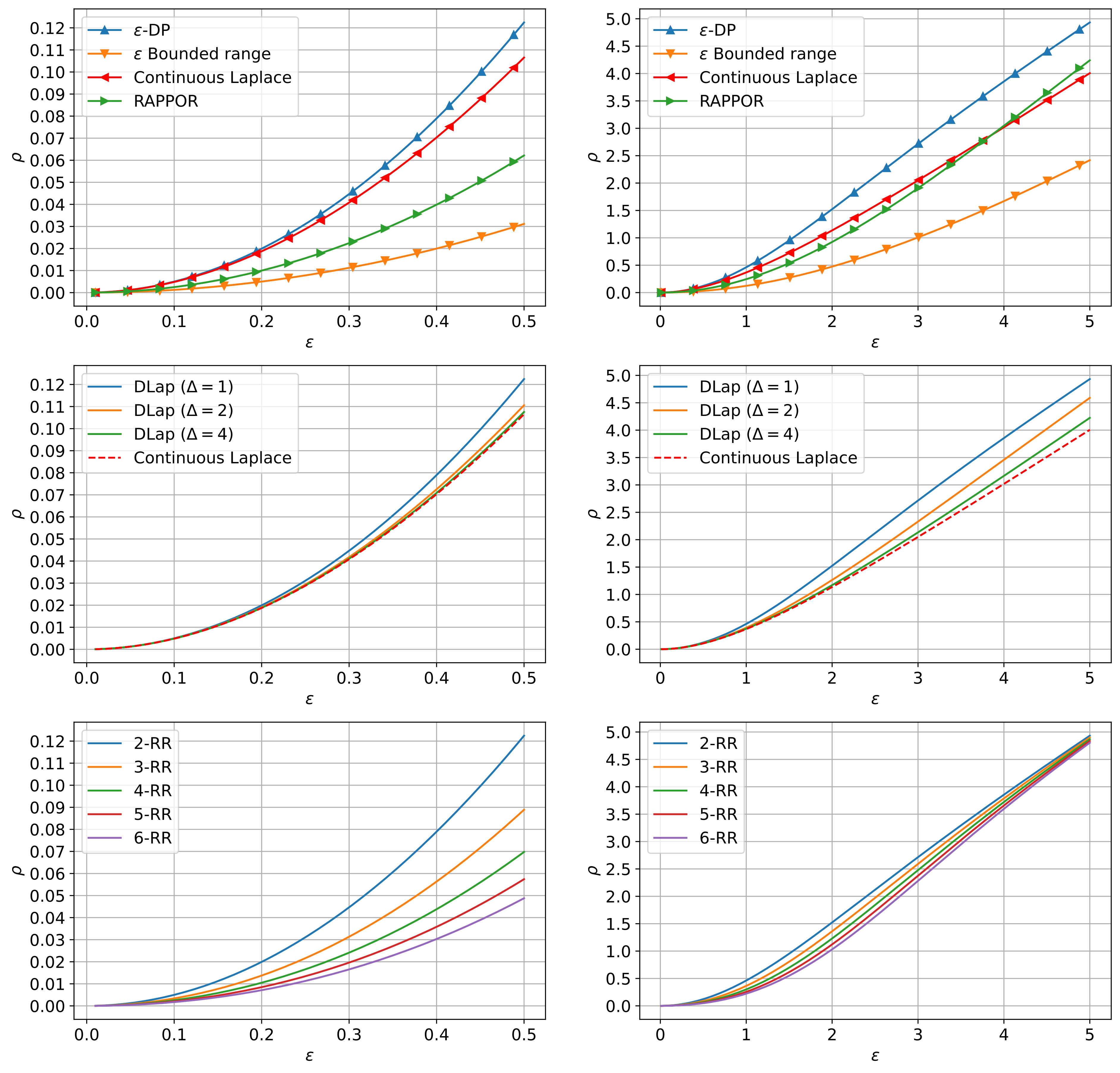
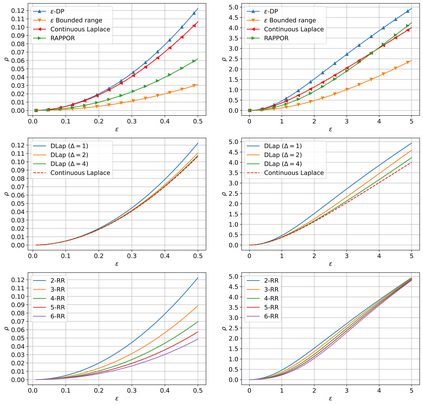
Zero-concentrated differential privacy (zCDP) is a variant of differential privacy (DP) that is widely used partly thanks to its nice composition property. While a tight conversion from $\epsilon$-DP to zCDP exists for the worst-case mechanism, many common algorithms satisfy stronger guarantees. In this work, we derive tight zCDP characterizations for several fundamental mechanisms. We prove that the tight zCDP bound for the $\epsilon$-DP Laplace mechanism is exactly $\epsilon + e^{-\epsilon} - 1$, confirming a recent conjecture by Wang (2022). We further provide tight bounds for the discrete Laplace mechanism, $k$-Randomized Response (for $k \leq 6$), and RAPPOR. Lastly, we also provide a tight zCDP bound for the worst case bounded range mechanism.

翻译：暂无翻译