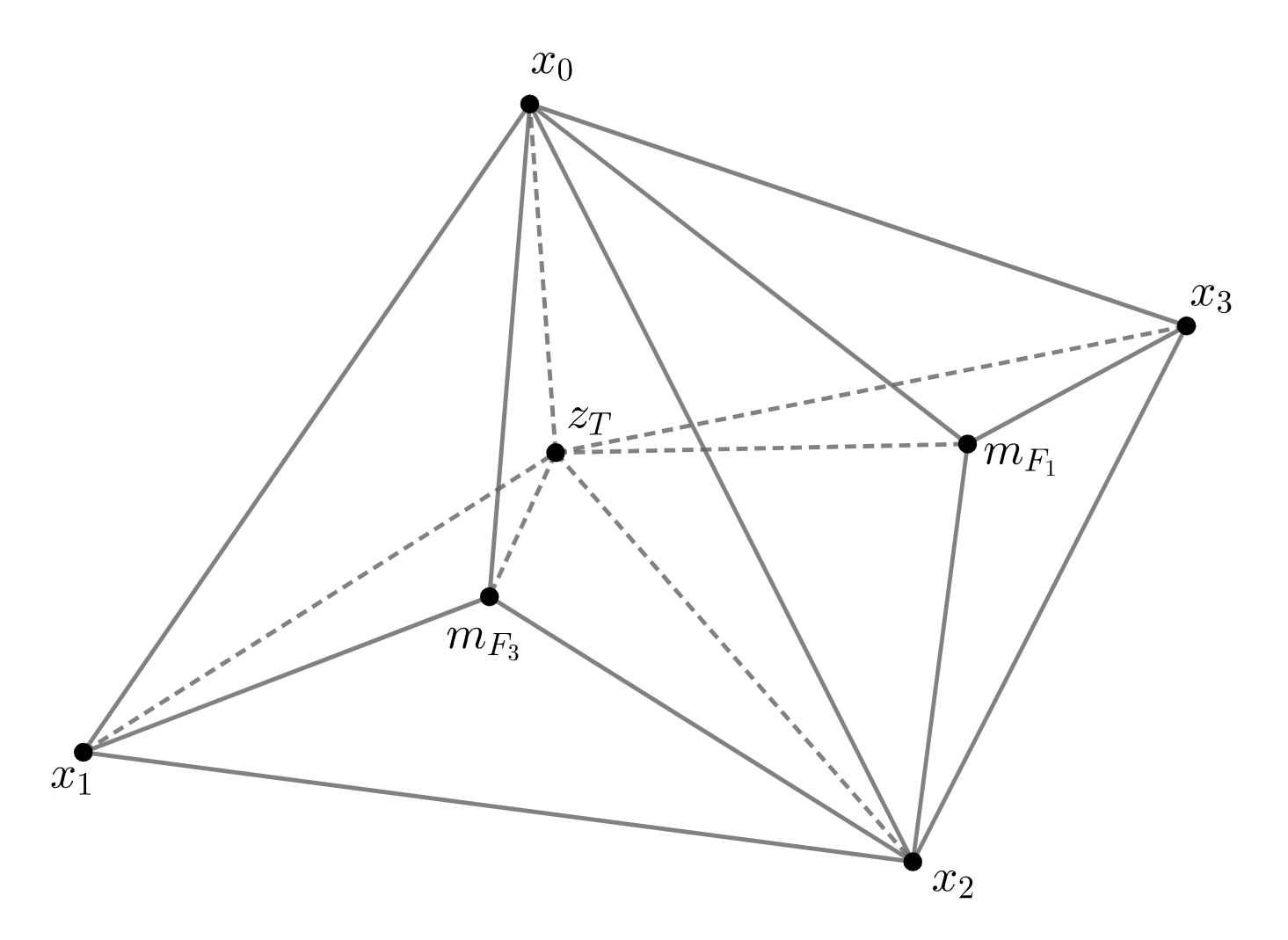
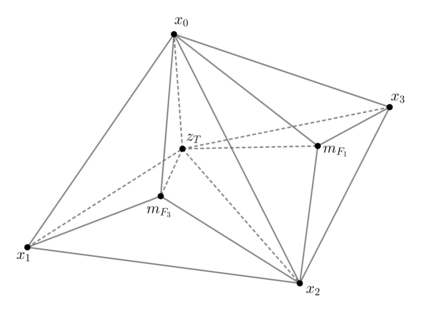
We construct several smooth finite element spaces defined on three--dimensional Worsey--Farin splits. In particular, we construct $C^1$, $H^1(\curl)$, and $H^1$-conforming finite element spaces and show the discrete spaces satisfy local exactness properties. A feature of the spaces is their low polynomial degree and lack of extrinsic supersmoothness at sub-simplices of the mesh. In the lowest order case, the last two spaces in the sequence consist of piecewise linear and piecewise constant spaces, and are suitable for the discretization of the (Navier-)Stokes equation.
翻译:我们用三维Worky-farin分割法来构建几个平滑的有限元素空间。特别是,我们建造了1美元、1美元(curl)和1美元(curl),并展示了离散空间符合本地精确性特性。一个特征是这些空间的多元度低,在网状的亚不易碎时缺乏外在超光谱。在最低顺序中,序列中的最后两个空间由条形线和条形不变空间组成,适合(Navier-Stokes)等式的离散化。