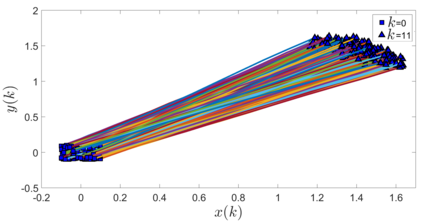
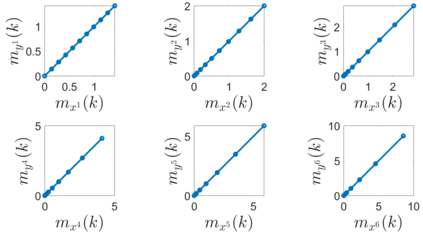
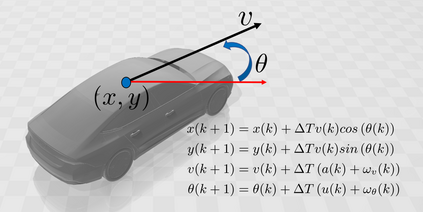
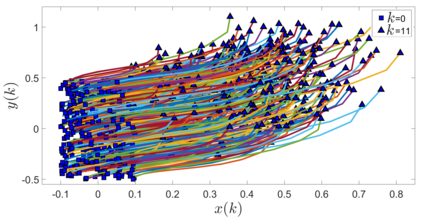
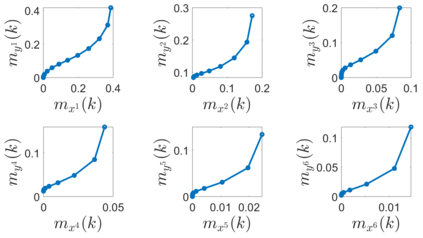
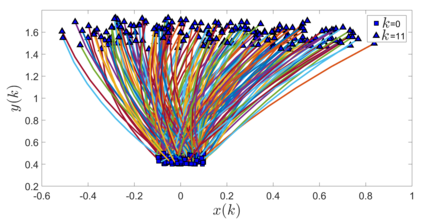
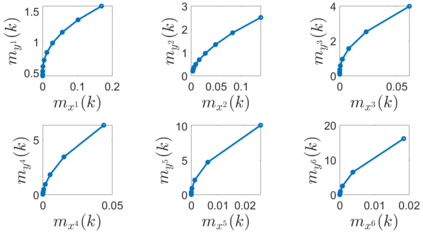
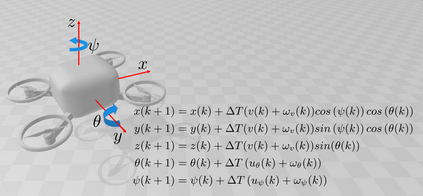
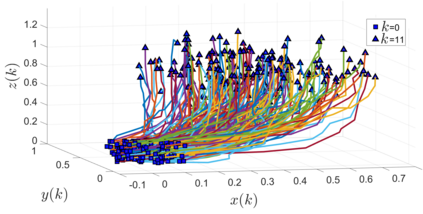
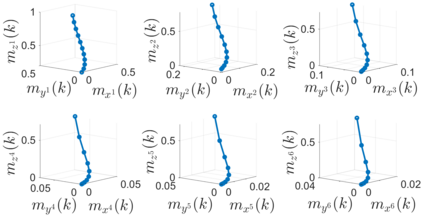
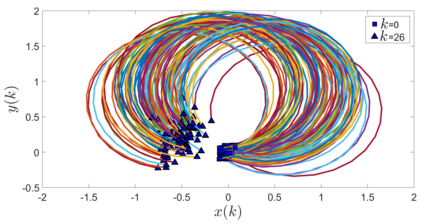
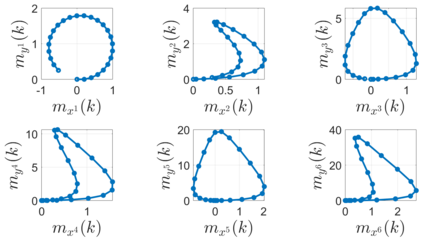
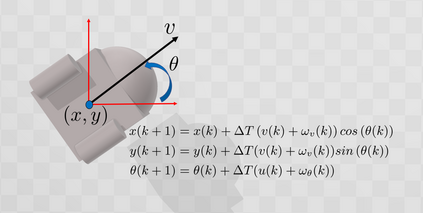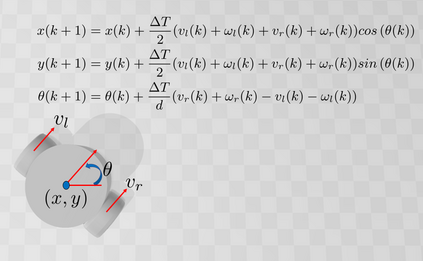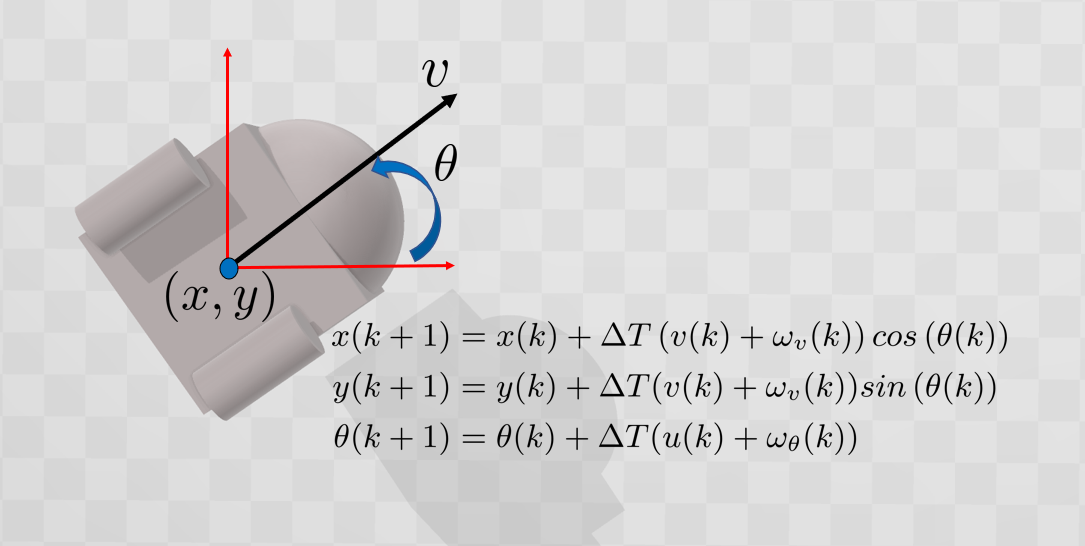In this paper, we address the problem of uncertainty propagation through nonlinear stochastic dynamical systems. More precisely, given a discrete-time continuous-state probabilistic nonlinear dynamical system, we aim at finding the sequence of the moments of the probability distributions of the system states up to any desired order over the given planning horizon. Moments of uncertain states can be used in estimation, planning, control, and safety analysis of stochastic dynamical systems. Existing approaches to address moment propagation problems provide approximate descriptions of the moments and are mainly limited to particular set of uncertainties, e.g., Gaussian disturbances. In this paper, to describe the moments of uncertain states, we introduce trigonometric and also mixed-trigonometric-polynomial moments. Such moments allow us to obtain closed deterministic dynamical systems that describe the exact time evolution of the moments of uncertain states of an important class of autonomous and robotic systems including underwater, ground, and aerial vehicles, robotic arms and walking robots. Such obtained deterministic dynamical systems can be used, in a receding horizon fashion, to propagate the uncertainties over the planning horizon in real-time. To illustrate the performance of the proposed method, we benchmark our method against existing approaches including linear, unscented transformation, and sampling based uncertainty propagation methods that are widely used in estimation, prediction, planning, and control problems.

翻译：在本文中,我们处理通过非线性随机动态系统传播不确定性的问题。更准确地说,鉴于一个离散的连续时间持续状态的概率性非线性动态系统,我们的目标是找到系统概率分布时间序列的顺序,直至特定规划视野的任何预期顺序。在估计、规划、控制和安全分析随机动态系统时,可以使用不确定状态的动力系统。现有解决瞬间传播问题的方法提供了对时间的大致描述,主要局限于特定的不确定状态,例如高萨扰动。在本文中,为了描述不确定状态的时刻,我们采用了三角测量和混为一流的测量-极性动态系统。这些时刻使我们能够获得封闭的确定性动态系统,描述一个重要类别的自主和机器人系统(包括水下、地面和航空飞行器、机器人和行走机器人)不确定状态的准确时间演变。这些获得的确定性动态系统可以用来在离地平线式时,用来描述不确定的状态,并用来广泛描述我们目前所使用的精确的预测方法,包括我们所使用的基准性分析方法。