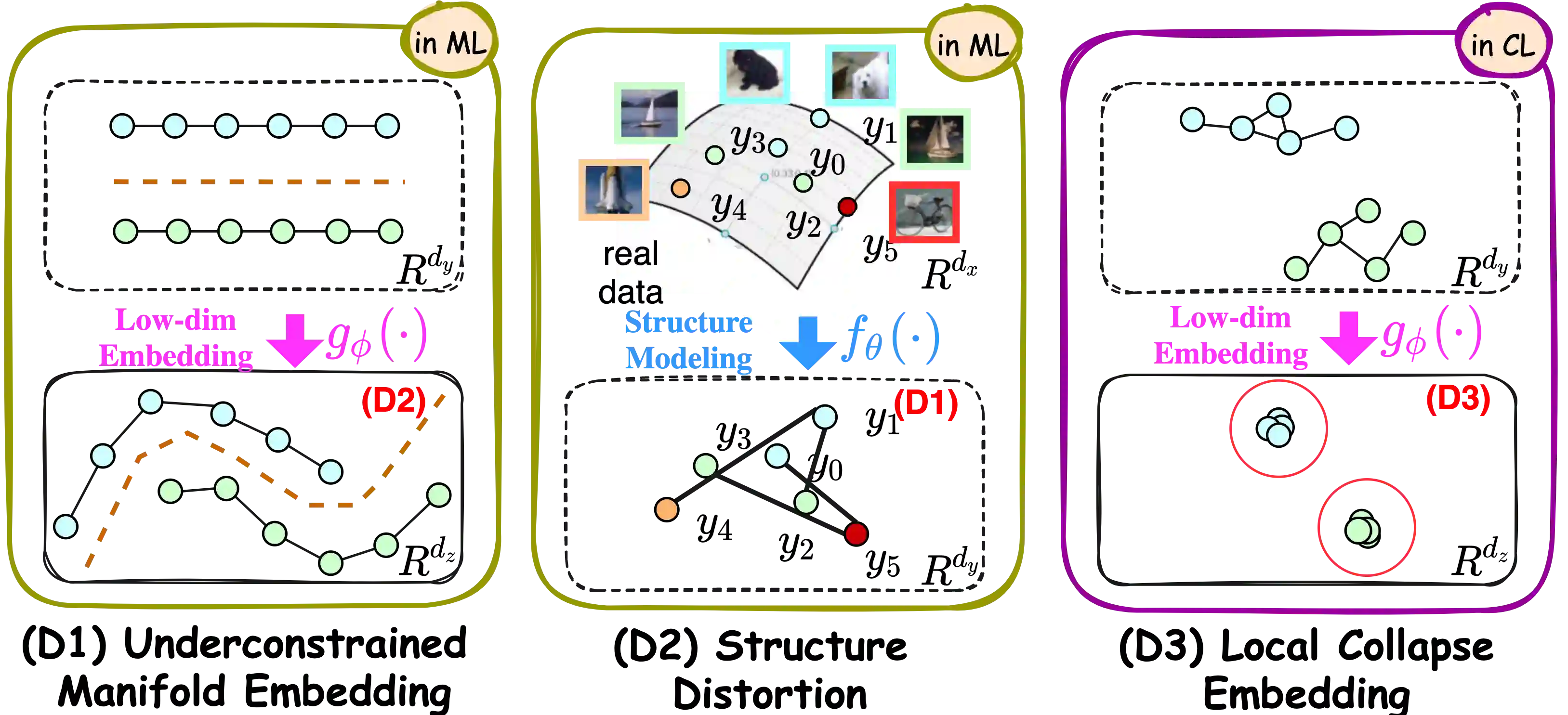
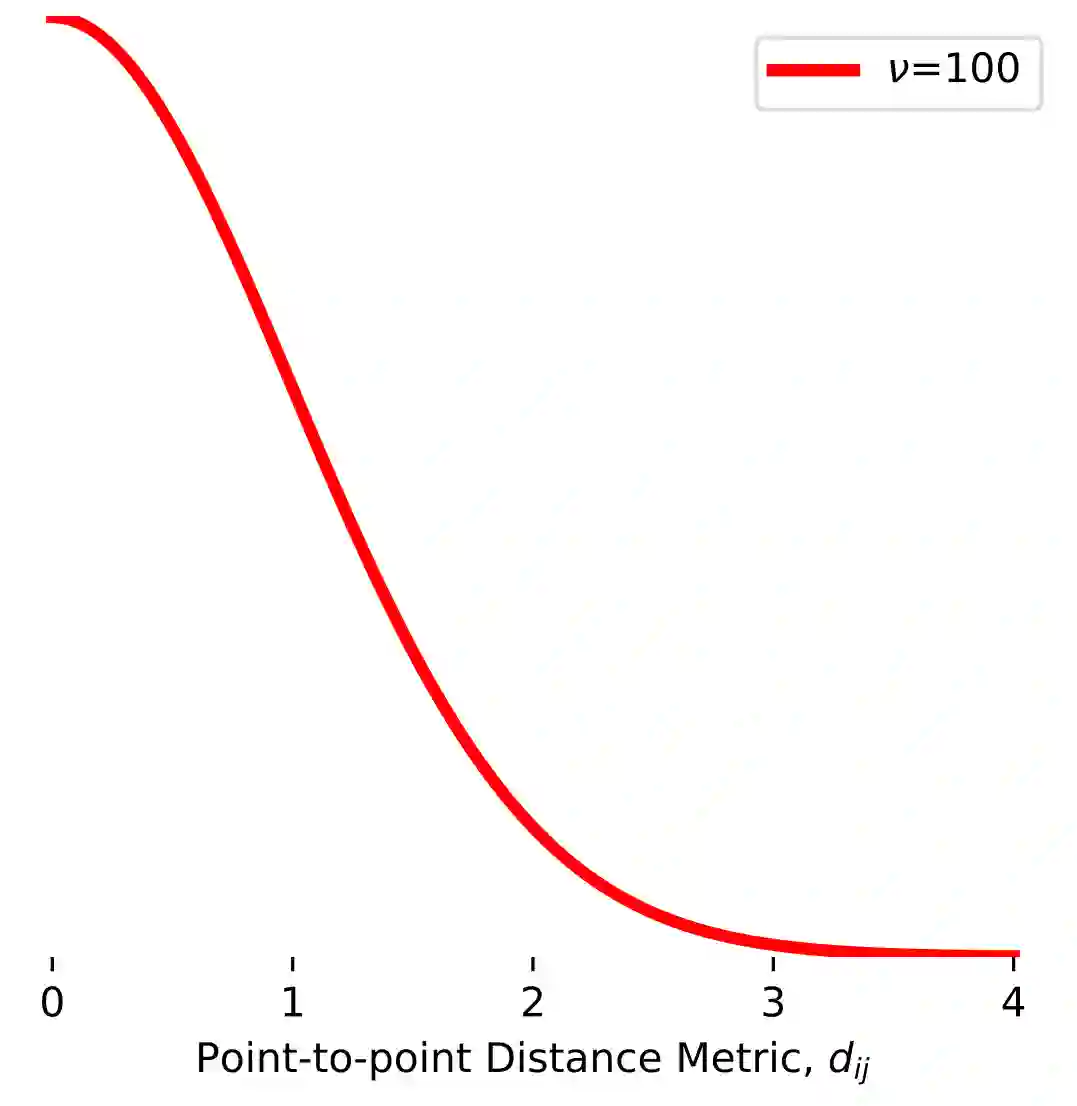
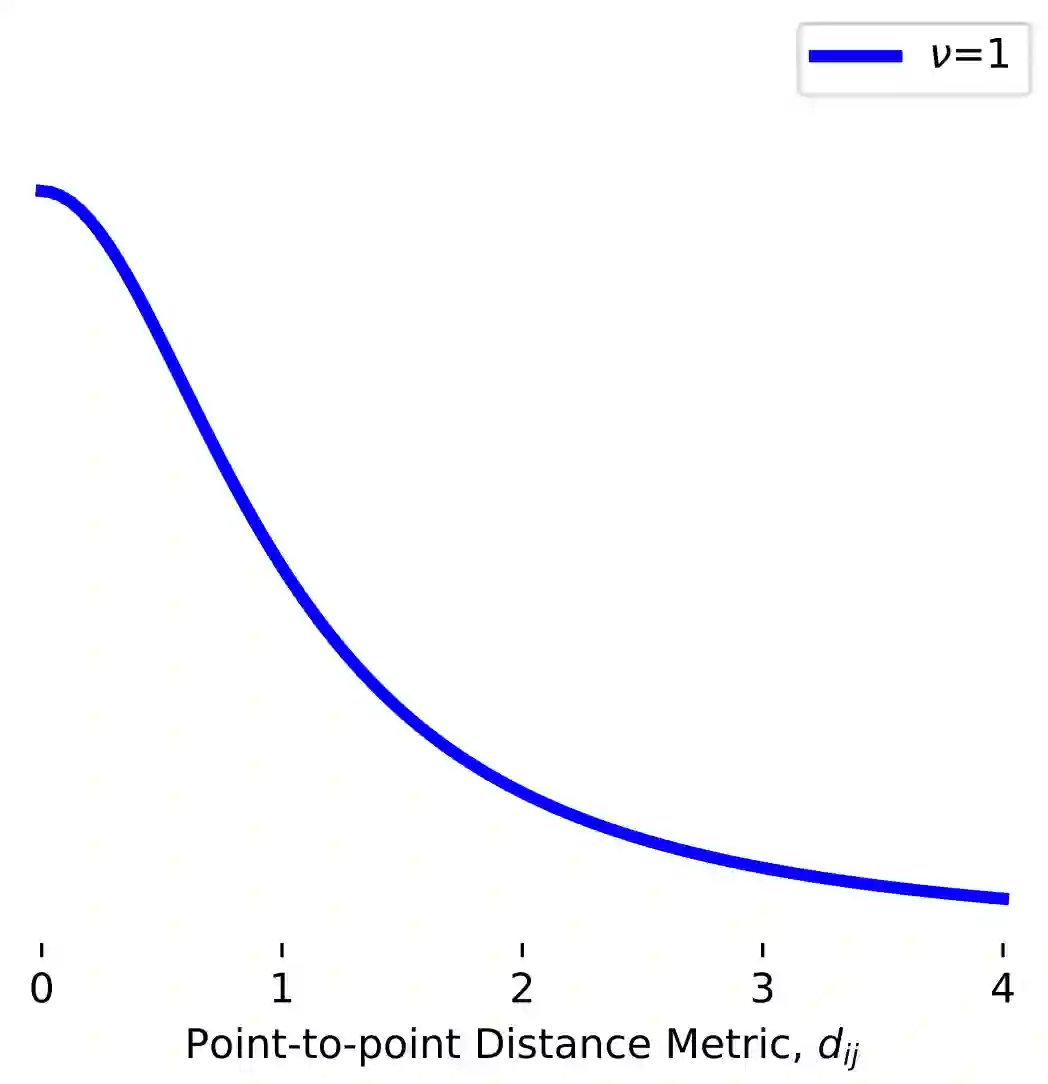
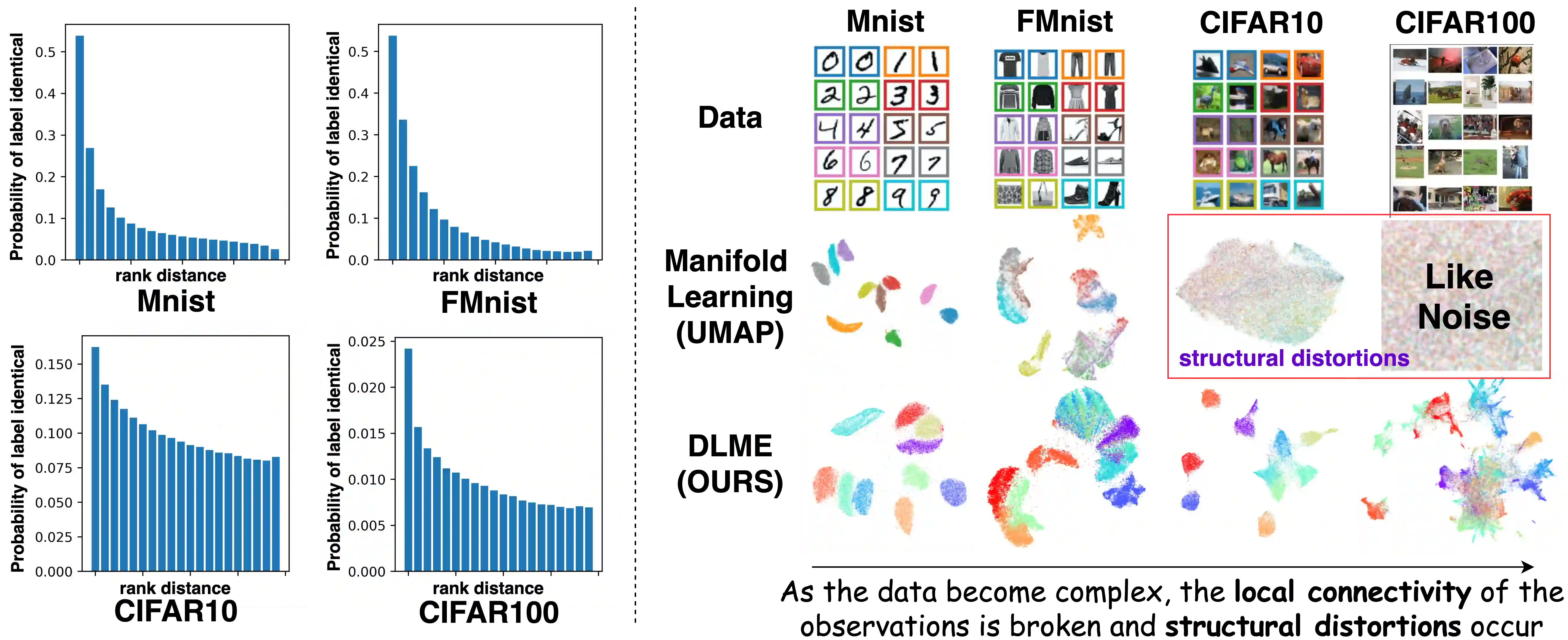
Manifold learning~(ML) aims to find low-dimensional embedding from high-dimensional data. Previous works focus on handcraft or easy datasets with simple and ideal scenarios; however, we find they perform poorly on real-world datasets with under-sampling data. Generally, ML methods primarily model data structure and subsequently process a low-dimensional embedding, where the poor local connectivity of under-sampling data in the former step and inappropriate optimization objectives in the later step will lead to \emph{structural distortion} and \emph{underconstrained embedding}. To solve this problem, we propose Deep Local-flatness Manifold Embedding (DLME), a novel ML framework to obtain reliable manifold embedding by reducing distortion. Our proposed DLME constructs semantic manifolds by data augmentation and overcomes \emph{structural distortion} problems with the help of its smooth framework. To overcome \emph{underconstrained embedding}, we design a specific loss for DLME and mathematically demonstrate that it leads to a more suitable embedding based on our proposed Local Flatness Assumption. In the experiments, by showing the effectiveness of DLME on downstream classification, clustering, and visualization tasks with three types of datasets (toy, biological, and image), our experimental results show that DLME outperforms SOTA ML \& contrastive learning (CL) methods.

翻译：Manidel 学习 ~ (ML) 的目的是从高维数据中找到低维嵌入 。 先前的工作重点是手工艺或简单易懂的数据集, 且有简单和理想的假想; 然而, 我们发现, 在含有低抽样数据的真实世界数据集上, 手工艺表现不力。 一般来说, ML 方法主要是模拟数据结构, 并随后处理一个低维嵌入程序, 在前步骤和后一步不适当的优化目标中, 取样不足的数据在本地连接不力, 会导致对比性扭曲 } 和\emph{ 不受约束的嵌入} 。 为了解决这个问题, 我们建议深本地缩缩缩缩缩嵌入 (DLME) 是一个全新的 ML 框架, 通过减少扭曲获得可靠的元嵌入。 我们提议的 DLME 通过数据增强和克服 平滑动框架的帮助, 设计一个特定的 DLME 和数学显示它导致更适合的嵌入性嵌入 3 TRA 。 我们提议的 DL 将显示我们的生物图像的模型, 显示 格式 显示我们的生物磁性 的图像 格式 。