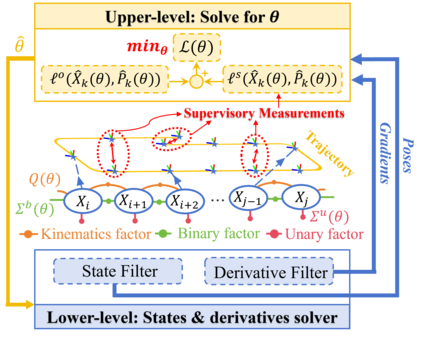
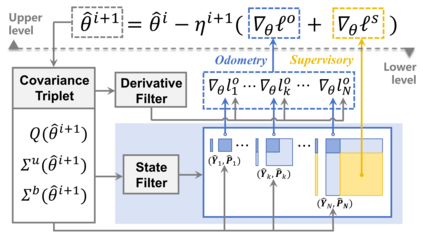
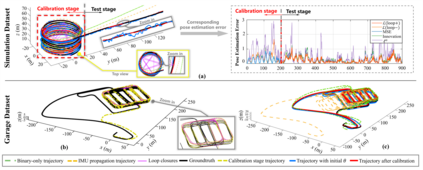
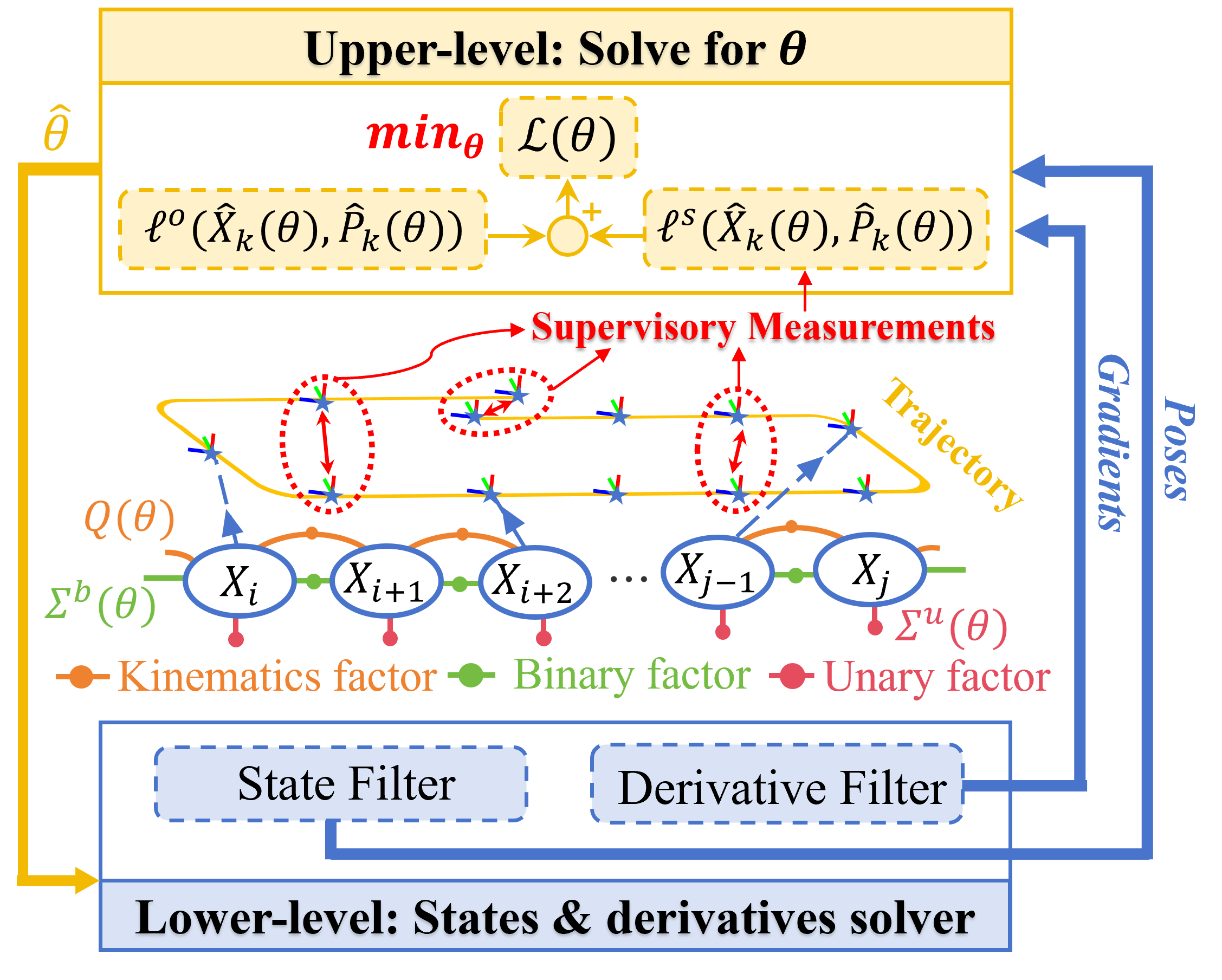
Reliable state estimation hinges on accurate specification of sensor noise covariances, which weigh heterogeneous measurements. In practice, these covariances are difficult to identify due to environmental variability, front-end preprocessing, and other reasons. We address this by formulating noise covariance estimation as a bilevel optimization that, from a Bayesian perspective, factorizes the joint likelihood of so-called odometry and supervisory measurements, thereby balancing information utilization with computational efficiency. The factorization converts the nested Bayesian dependency into a chain structure, enabling efficient parallel computation: at the lower level, an invariant extended Kalman filter with state augmentation estimates trajectories, while a derivative filter computes analytical gradients in parallel for upper-level gradient updates. The upper level refines the covariance to guide the lower-level estimation. Experiments on synthetic and real-world datasets show that our method achieves higher efficiency over existing baselines.

翻译：暂无翻译