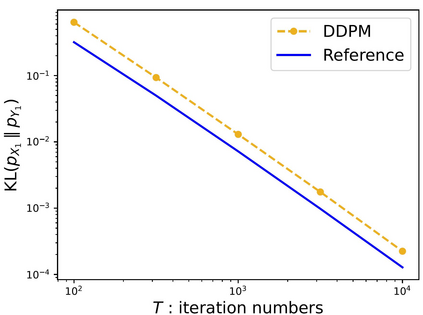
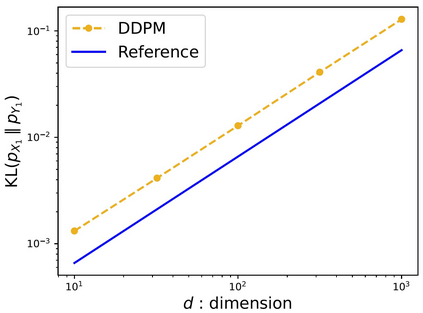
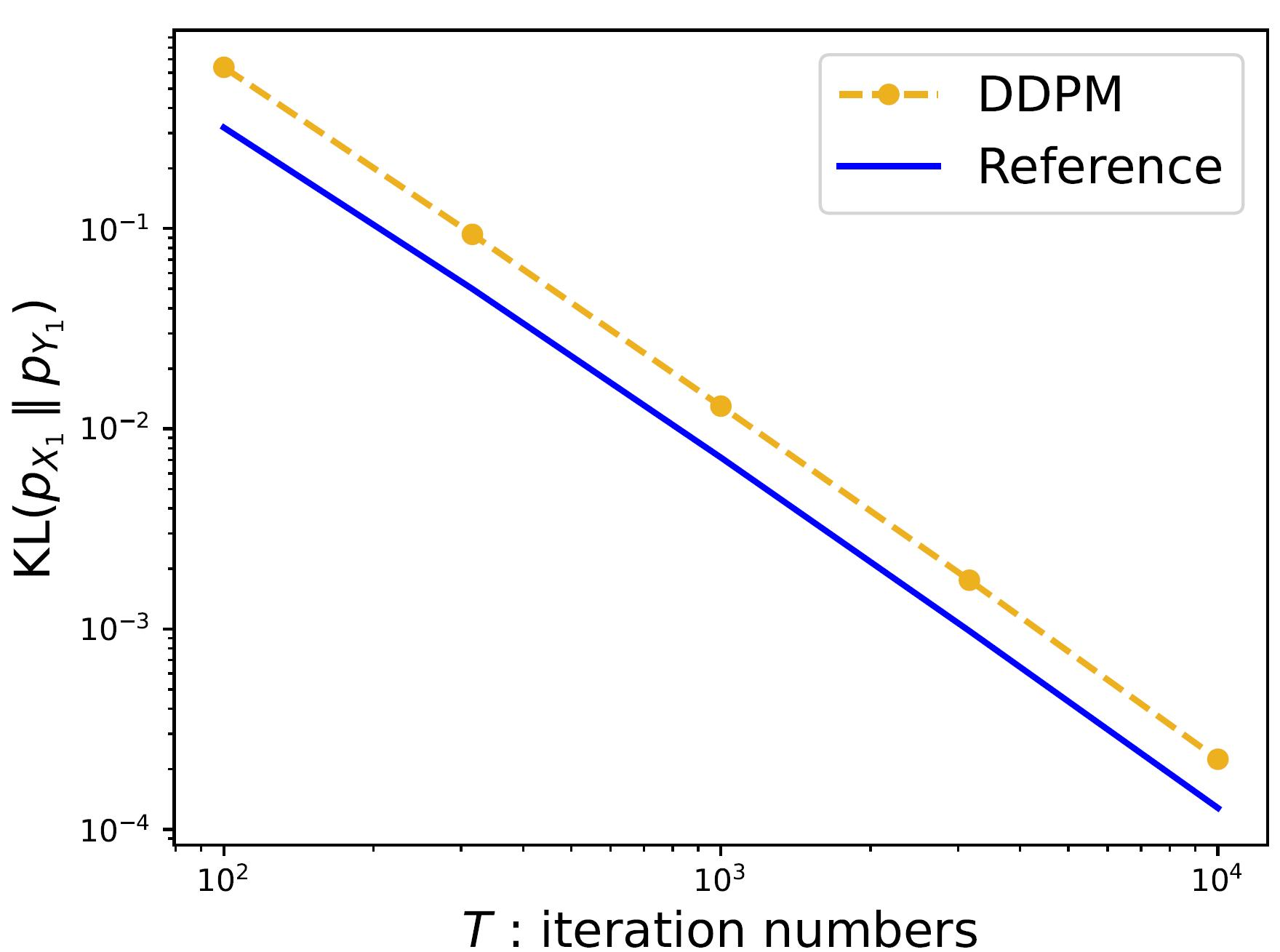
Score-based diffusion models have achieved remarkable empirical success in generating high-quality samples from target data distributions. Among them, the Denoising Diffusion Probabilistic Model (DDPM) is one of the most widely used samplers, generating samples via estimated score functions. Despite its empirical success, a tight theoretical understanding of DDPM -- especially its convergence properties -- remains limited. In this paper, we provide a refined convergence analysis of the DDPM sampler and establish near-optimal convergence rates under general distributional assumptions. Specifically, we introduce a relaxed smoothness condition parameterized by a constant $L$, which is small for many practical distributions (e.g., Gaussian mixture models). We prove that the DDPM sampler with accurate score estimates achieves a convergence rate of $$\widetilde{O}\left(\frac{d\min\{d,L^2\}}{T^2}\right)~\text{in Kullback-Leibler divergence},$$ where $d$ is the data dimension, $T$ is the number of iterations, and $\widetilde{O}$ hides polylogarithmic factors in $T$. This result substantially improves upon the best-known $d^2/T^2$ rate when $L < \sqrt{d}$. By establishing a matching lower bound, we show that our convergence analysis is tight for a wide array of target distributions. Moreover, it reveals that DDPM and DDIM share the same dependence on $d$, raising an interesting question of why DDIM often appears empirically faster.

翻译：暂无翻译