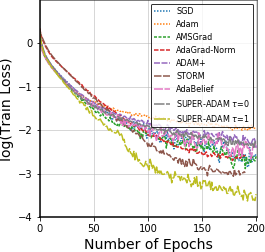
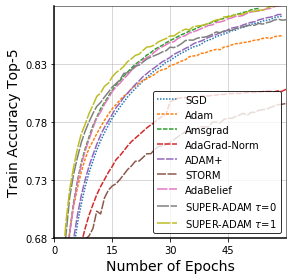
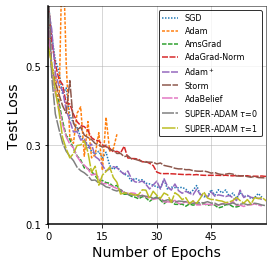
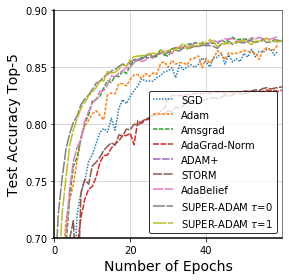
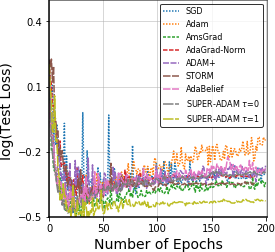
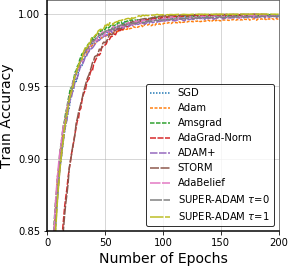
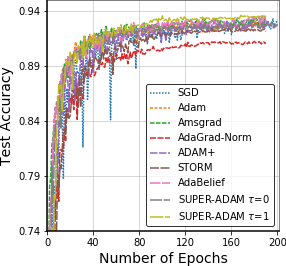
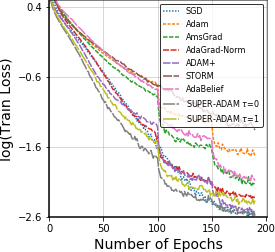
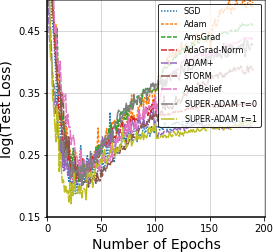
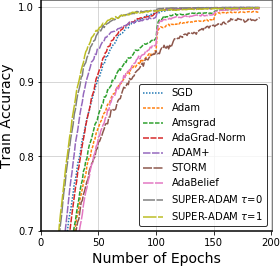
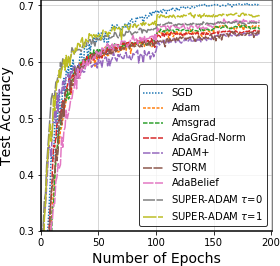
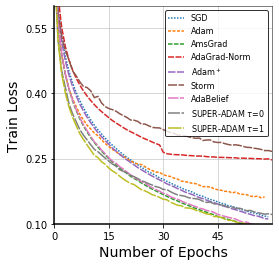
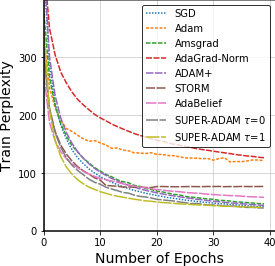
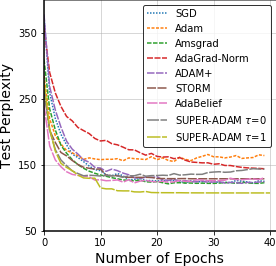
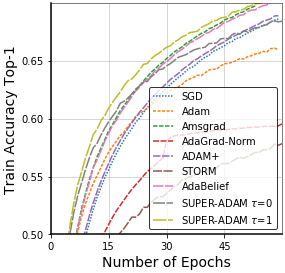
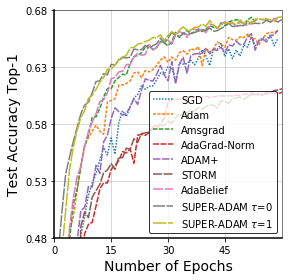
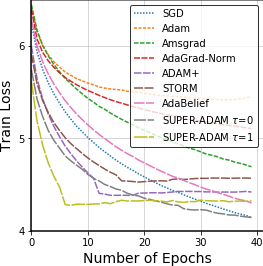
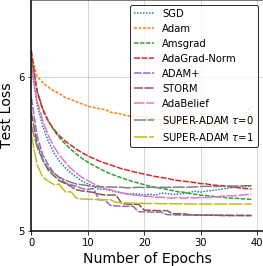
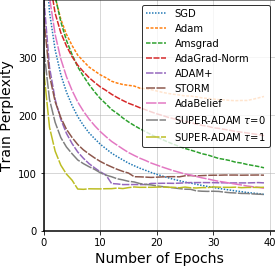
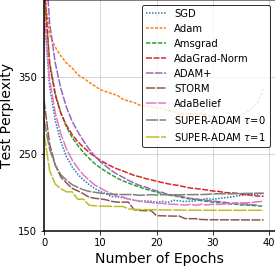
Adaptive gradient methods have shown excellent performances for solving many machine learning problems. Although multiple adaptive gradient methods were recently studied, they mainly focus on either empirical or theoretical aspects and also only work for specific problems by using some specific adaptive learning rates. Thus, it is desired to design a universal framework for practical algorithms of adaptive gradients with theoretical guarantee to solve general problems. To fill this gap, we propose a faster and universal framework of adaptive gradients (i.e., SUPER-ADAM) by introducing a universal adaptive matrix that includes most existing adaptive gradient forms. Moreover, our framework can flexibly integrate the momentum and variance reduced techniques. In particular, our novel framework provides the convergence analysis support for adaptive gradient methods under the nonconvex setting. In theoretical analysis, we prove that our SUPER-ADAM algorithm can achieve the best known gradient (i.e., stochastic first-order oracle (SFO)) complexity of $\tilde{O}(\epsilon^{-3})$ for finding an $\epsilon$-stationary point of nonconvex optimization, which matches the lower bound for stochastic smooth nonconvex optimization. In numerical experiments, we employ various deep learning tasks to validate that our algorithm consistently outperforms the existing adaptive algorithms. Code is available at https://github.com/LIJUNYI95/SuperAdam

翻译：尽管最近研究了多种适应性梯度方法,但它们主要侧重于经验或理论方面,并且仅通过使用某些特定的适应性学习率来应对具体问题。因此,我们希望设计一个通用的适应性梯度实用算法框架,在理论上保证解决一般问题。为了填补这一空白,我们建议一个更快捷和通用的适应性梯度(即SUPER-ADM)框架框架,引入一个包含大多数现有适应性梯度形式的通用适应性矩阵。此外,我们的框架可以灵活地整合动力和差异减少技术。特别是,我们的新框架为非convex设置下的适应性梯度方法提供了趋同分析支持。在理论分析中,我们证明我们的SUPER-ADAM算法能够达到已知的最佳梯度(即,先等级级或末级(SFO))复杂度(即SUPER-ADAM)框架,以寻找一个$(eepslon)/固定的不convex优化点,该点与用于稳定性测试的低约束性测试系统/CLAFAFA, 以持续、Stocal化、ADLisformacialstrismastrismstris