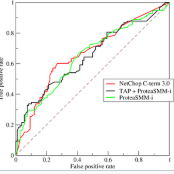
The ROC-SVM, originally proposed by Rakotomamonjy, directly maximizes the area under the ROC curve (AUC) and has become an attractive alternative of the conventional binary classification under the presence of class imbalance. However, its practical use is limited by high computational cost, as training involves evaluating all $O(n^2)$. To overcome this limitation, we develop a scalable variant of the ROC-SVM that leverages incomplete U-statistics, thereby substantially reducing computational complexity. We further extend the framework to nonlinear classification through a low-rank kernel approximation, enabling efficient training in reproducing kernel Hilbert spaces. Theoretical analysis establishes an error bound that justifies the proposed approximation, and empirical results on both synthetic and real datasets demonstrate that the proposed method achieves comparable AUC performance to the original ROC-SVM with drastically reduced training time.
翻译:ROC-SVM最初由Rakotomamonjy提出,直接最大化受试者工作特征曲线下面积(AUC),在类别不平衡情况下已成为传统二分类方法的有力替代方案。然而,其实际应用受限于高昂的计算成本,因为训练过程需要评估所有$O(n^2)$个样本对。为突破此限制,我们开发了一种基于不完全U统计量的可扩展ROC-SVM变体,显著降低了计算复杂度。我们进一步通过低秩核近似将该框架扩展至非线性分类,实现了在再生核希尔伯特空间中的高效训练。理论分析建立了误差界以证明所提近似的合理性,在合成与真实数据集上的实证结果表明,该方法在保持与原始ROC-SVM相当的AUC性能的同时,大幅减少了训练时间。