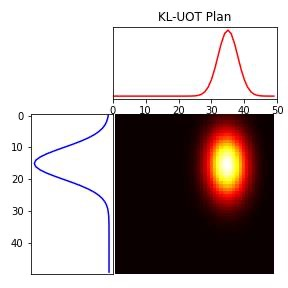
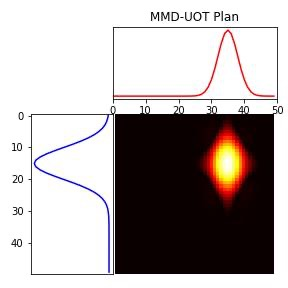
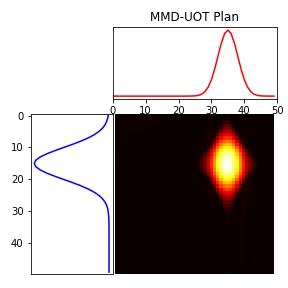
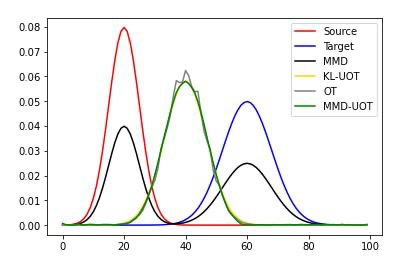
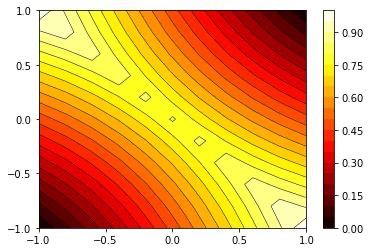
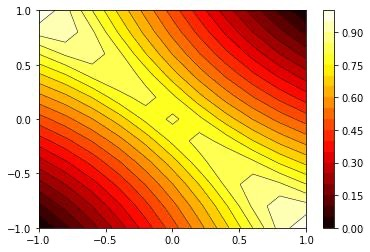
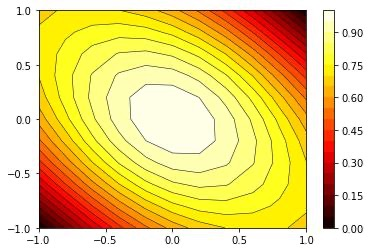
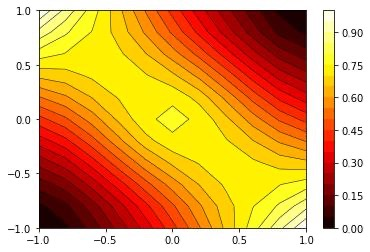
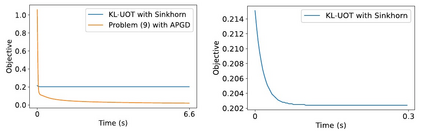
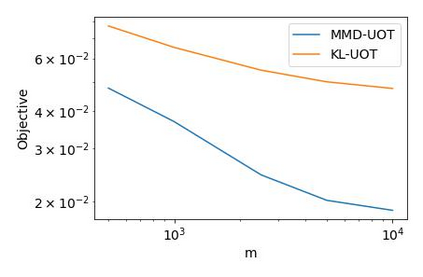
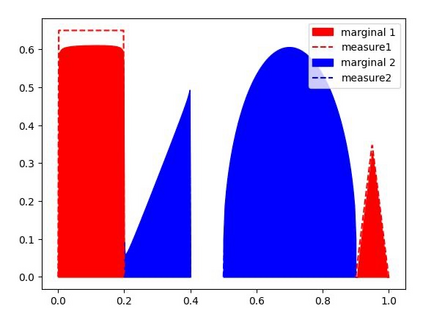
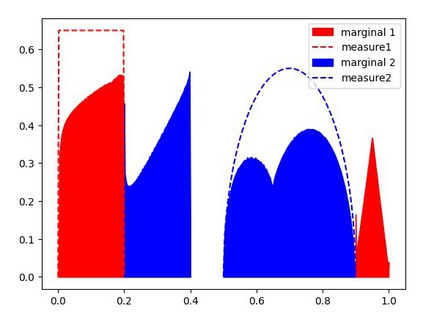
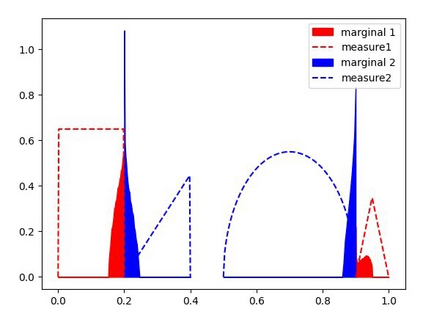
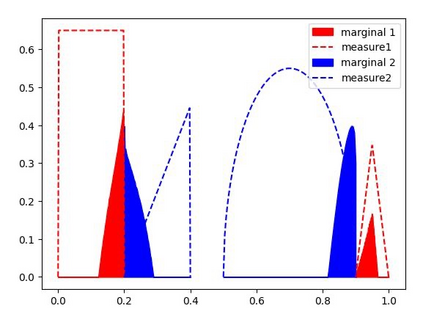
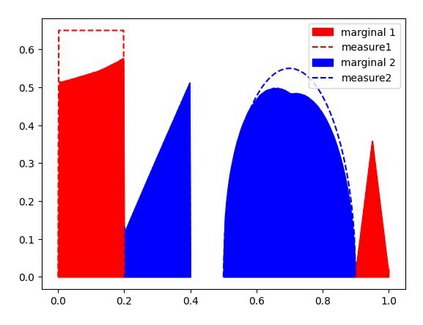
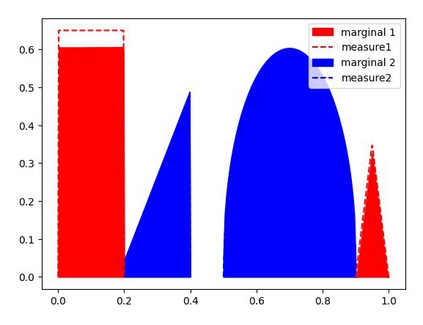
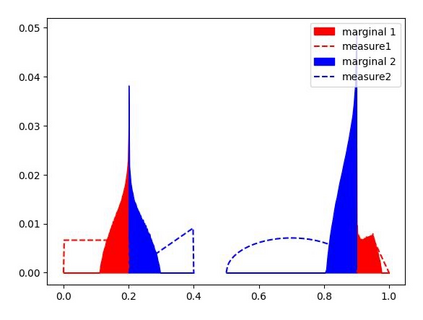
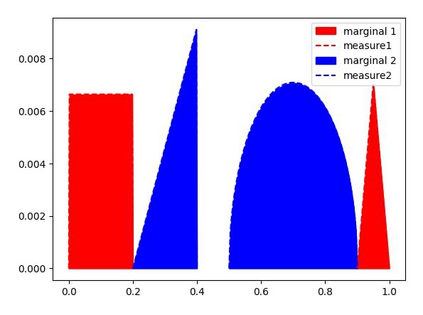
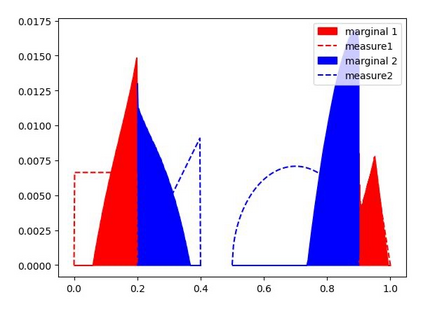
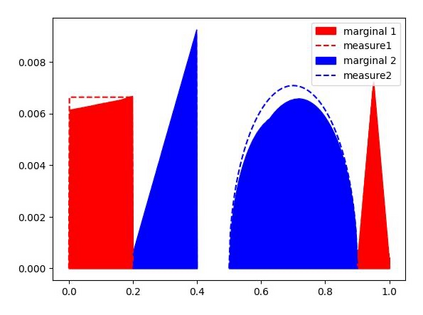
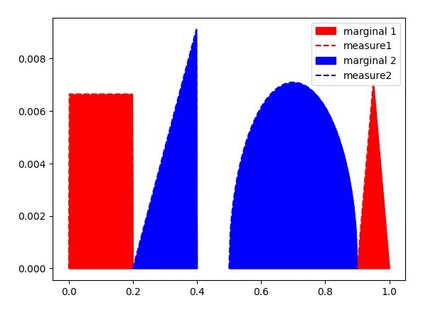
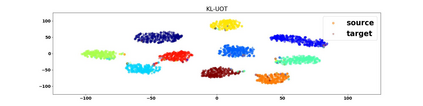
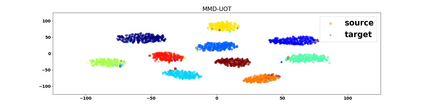
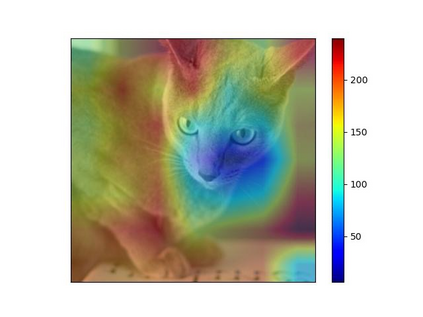
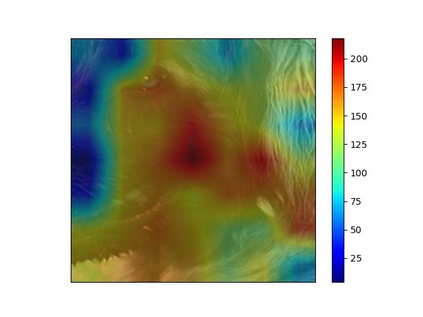
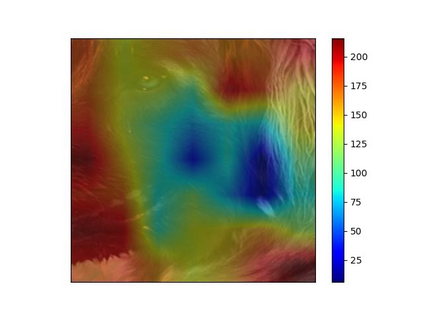
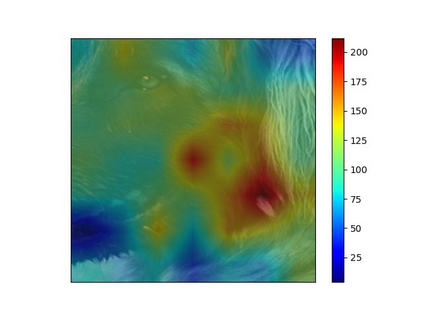
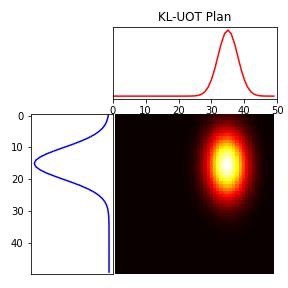
We study the unbalanced optimal transport (UOT) problem, where the marginal constraints are enforced using Maximum Mean Discrepancy (MMD) regularization. Our work is motivated by the observation that the literature on UOT is focused on regularization based on $\phi$-divergence (e.g., KL divergence). Despite the popularity of MMD, its role as a regularizer in the context of UOT seems less understood. We begin by deriving a specific dual of MMD-regularized UOT (MMD-UOT), which helps us prove several useful properties. One interesting outcome of this duality result is that MMD-UOT induces novel metrics, which not only lift the ground metric like the Wasserstein but are also sample-wise efficient to estimate like the MMD. Further, for real-world applications involving non-discrete measures, we present an estimator for the transport plan that is supported only on the given ($m$) samples. Under certain conditions, we prove that the estimation error with this finitely-supported transport plan is also $\mathcal{O}(1/\sqrt{m})$. As far as we know, such error bounds that are free from the curse of dimensionality are not known for $\phi$-divergence regularized UOT. Finally, we discuss how the proposed estimator can be computed efficiently using accelerated gradient descent. Our experiments show that MMD-UOT consistently outperforms popular baselines, including KL-regularized UOT and MMD, in diverse machine learning applications. Our codes are publicly available at https://github.com/Piyushi-0/MMD-reg-OT

翻译：暂无翻译