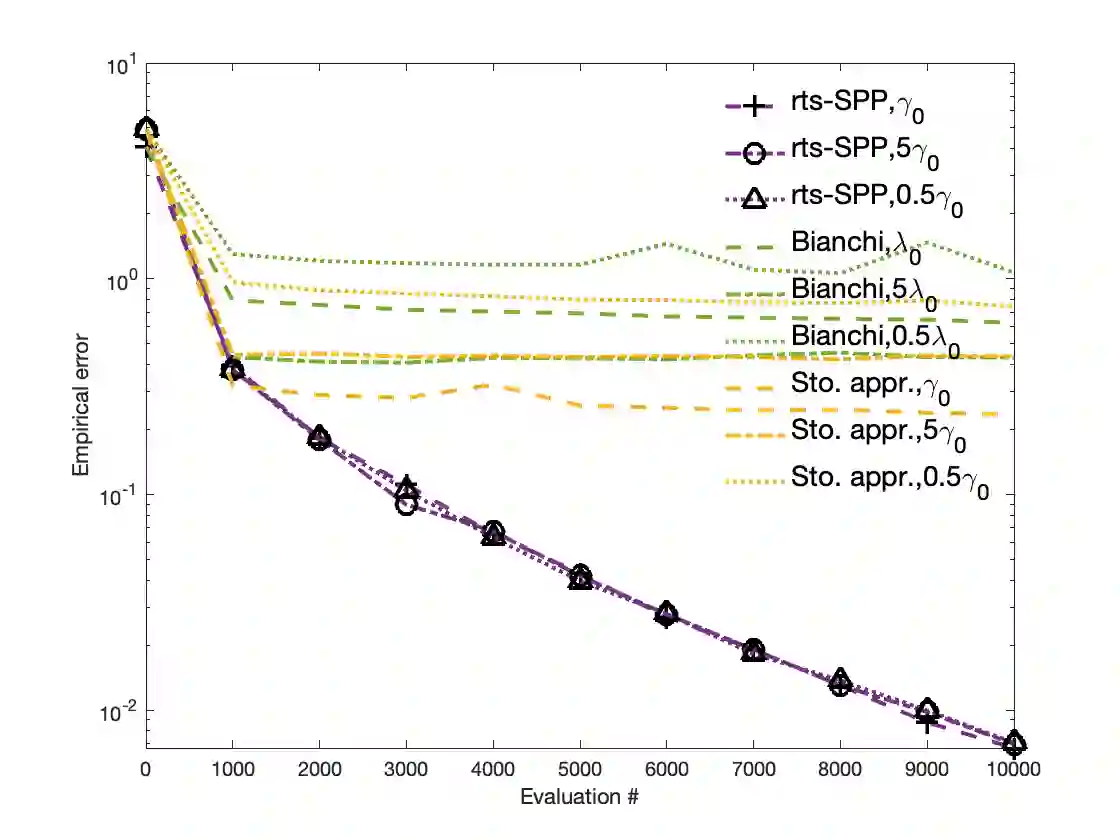
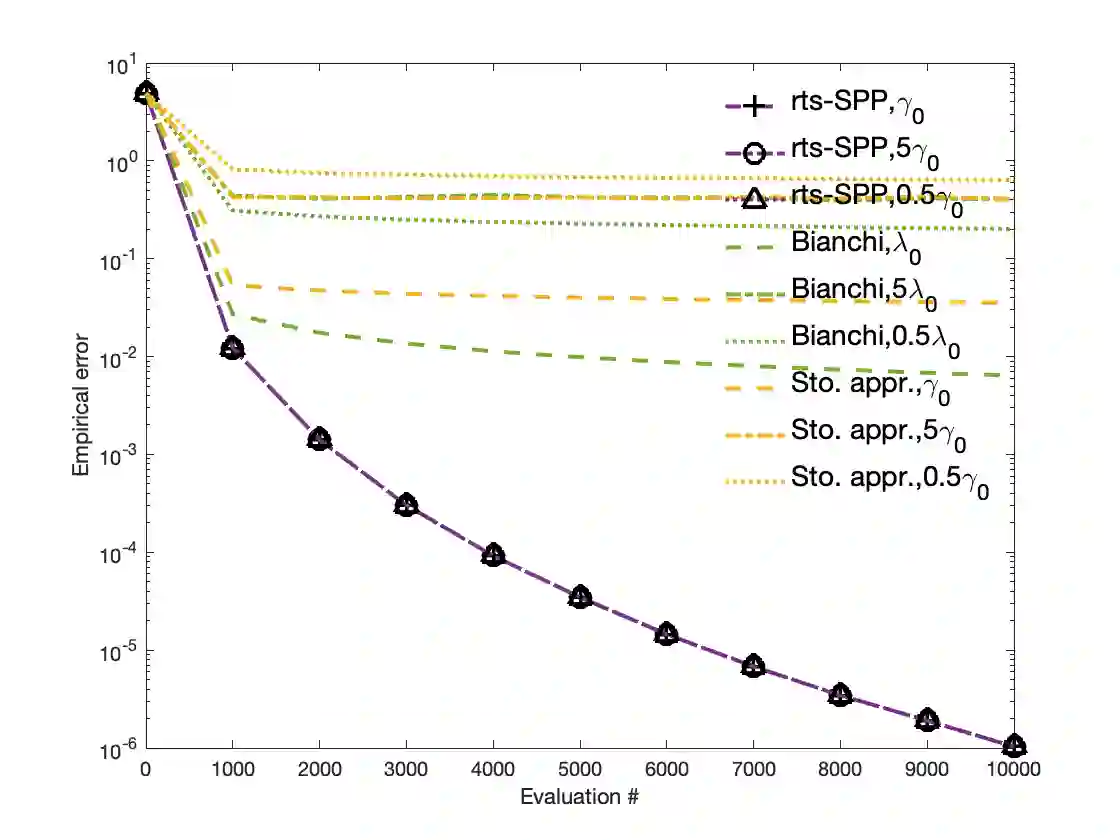
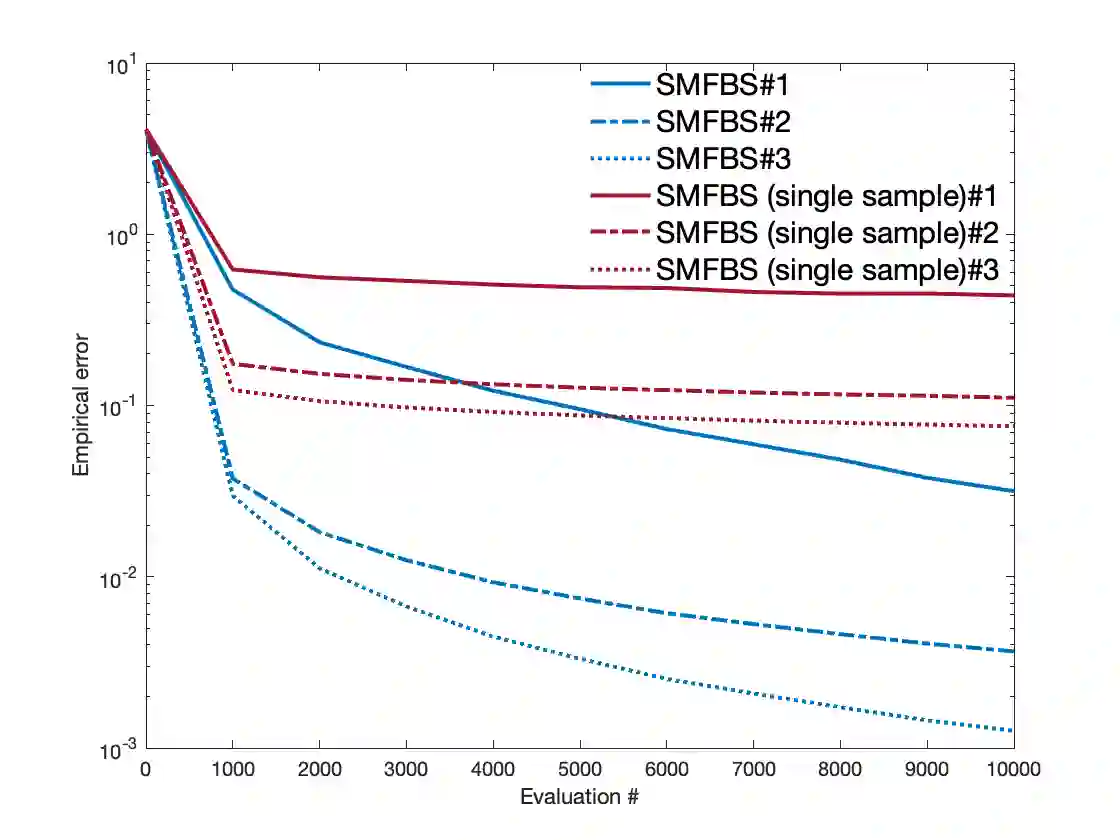
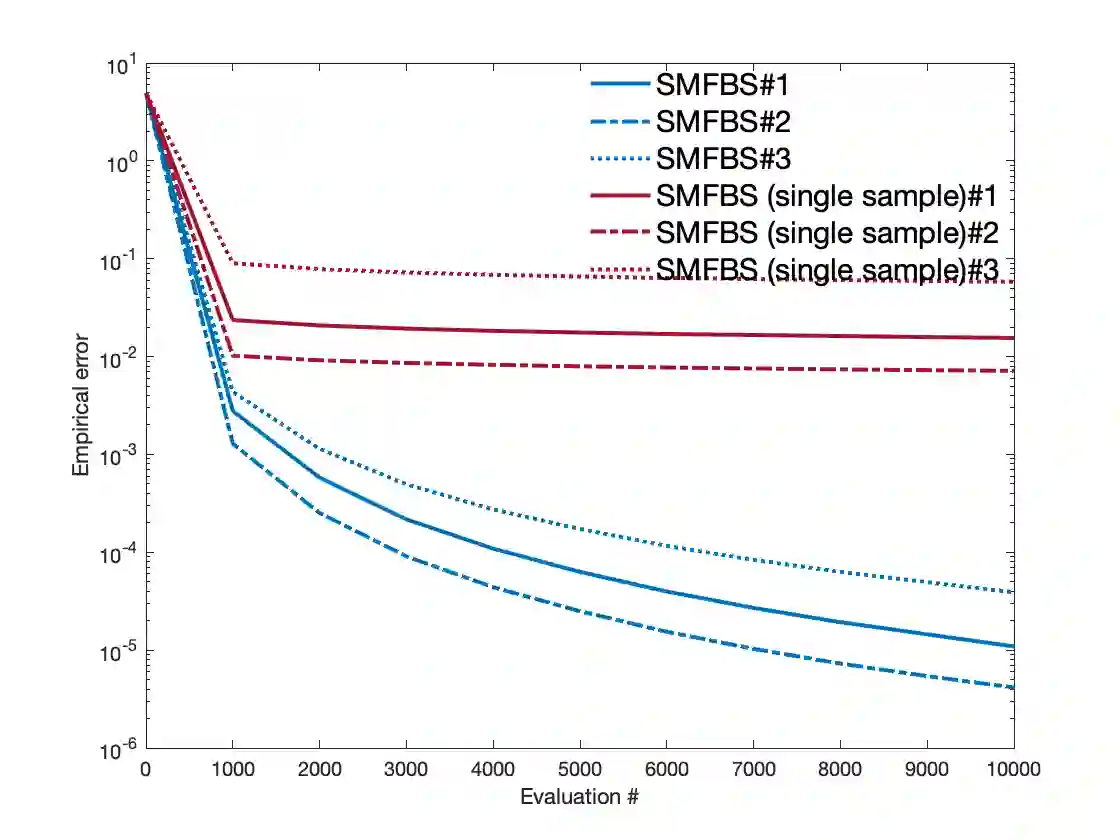
We consider monotone inclusion problems where the operators may be expectation-valued. A direct application of proximal and splitting schemes is complicated by resolving problems with expectation-valued maps at each step, a concern that is addressed by using sampling. Accordingly, we propose avenues for addressing uncertainty in the mapping. (i) Variance-reduced stochastic proximal point method (vr-SPP). We develop amongst the first variance-reduced stochastic proximal-point schemes that achieves deterministic rates of convergence in terms of solving proximal-point problems. In addition, it is shown that the schemes are characterized by either optimal or near-optimal oracle (or sample) complexity guarantees. Finally, the generated sequences are shown to be convergent to a solution in an almost-sure sense in both monotone and strongly monotone regimes; (ii) Variance-reduced stochastic modified forward-backward splitting scheme (vr-SMFBS). In constrained settings, we consider structured settings when the map can be decomposed into an expectation-valued map $A$ and a maximal monotone map $B$ with a tractable resolvent. Akin to (i), we show that the proposed schemes are equipped with a.s. convergence guarantees, linear (strongly monotone $A$) and $\mathcal{O}(1/k)$ (monotone $A$) rates of convergence while achieving optimal oracle complexity bounds. Of these, the rate statements in monotone regimes rely on leveraging the Fitzpatrick gap function for monotone inclusions. Furthermore, the schemes rely on weaker moment requirements on noise as well as allow for weakening unbiasedness requirements on oracles in strongly monotone regimes. Preliminary numerics reflect these findings and show that the variance-reduced schemes outperform stochastic approximation schemes, stochastic splitting and proximal point schemes, and sample-average approximation approaches.

翻译：我们考虑单调融入问题,操作员可能会在其中获得预期价值。 直接应用准度和分解计划,通过解决每步的期待值地图问题而变得复杂, 这一问题是通过抽样解决的。 因此, 我们提出在绘图中解决不确定性的渠道。 (一) 差异减少的随机准点方法(vr-SPP) 。 我们在第一个差异减少的随机偏差准点计划中开发出在解决准度问题方面达到确定性比率的混合点计划。 (vr-SMFBS) 在受约束的环境下, 当地图可以分解为预期值的平价地图($A) 或近于最优化的(或抽样) 复杂性保证生成的序列在单调和强烈的单调机制中几乎具有确定性意义; (二) 差异减少的随机偏差调整的前向后向分裂计划(vr-SMFBS), 在受约束的环境下,我们考虑结构化的设置, 当地图可以分解成一个预期值的美分值的正值地图($) 。