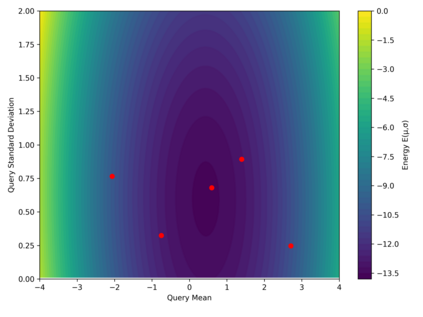
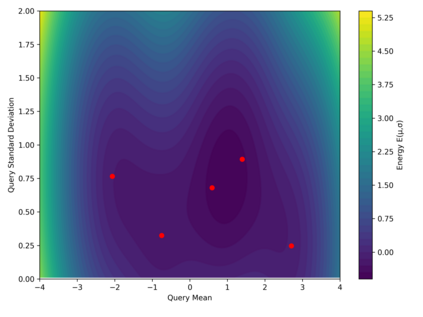
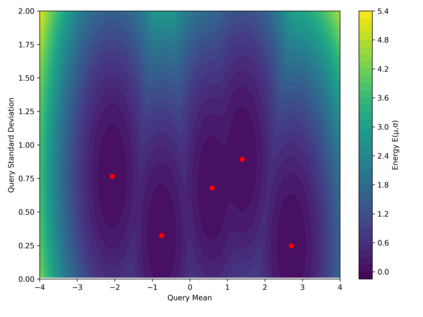
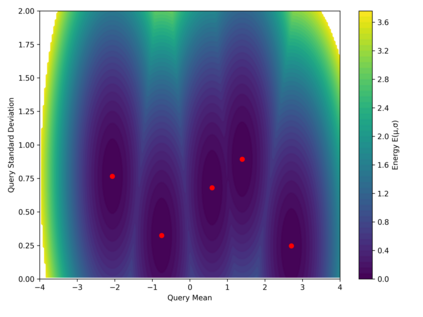
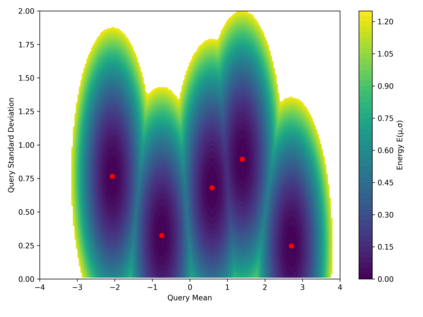
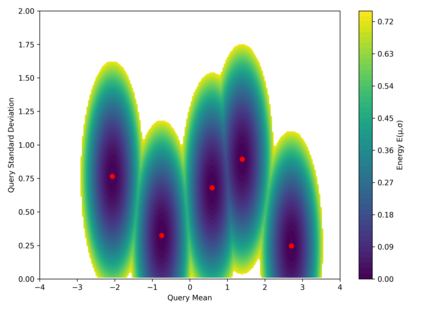
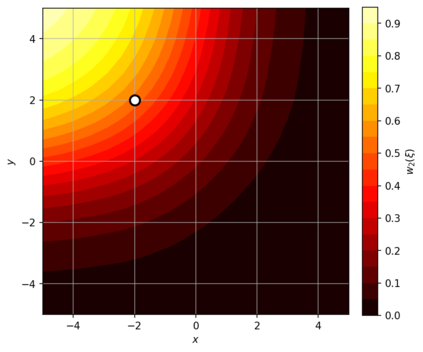
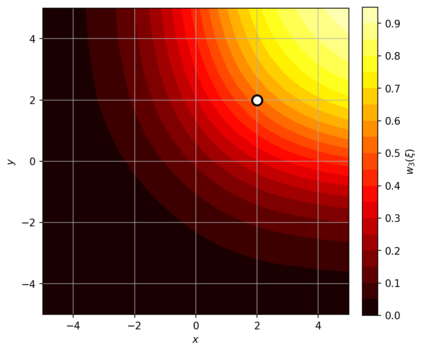
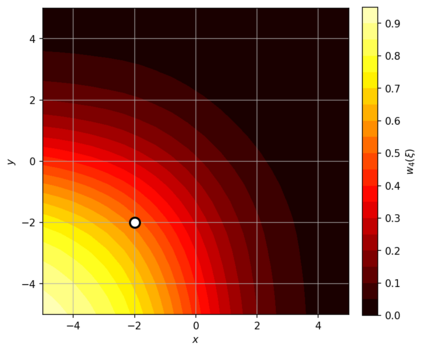
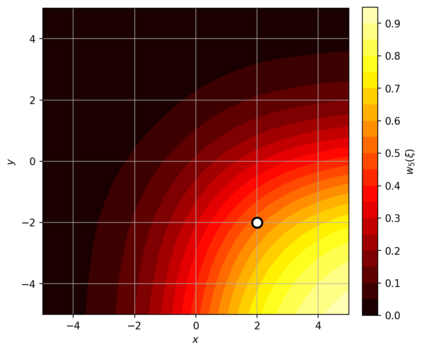
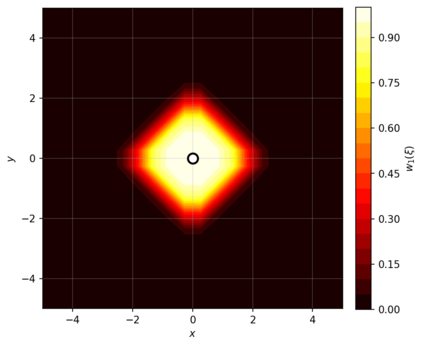
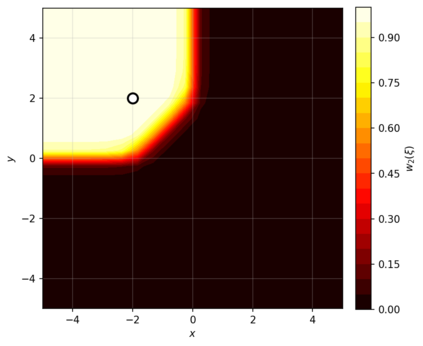
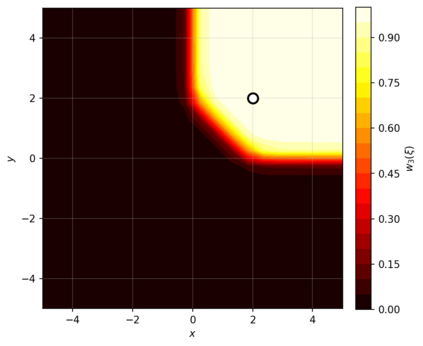
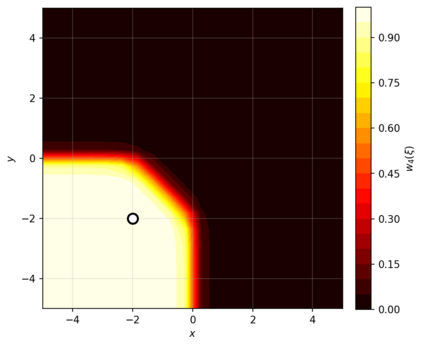
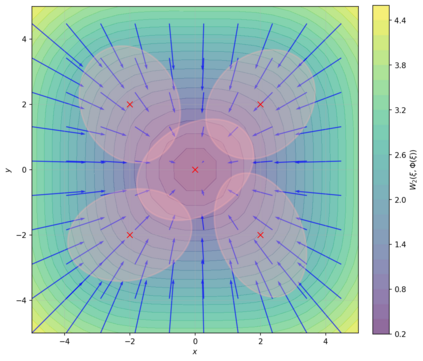
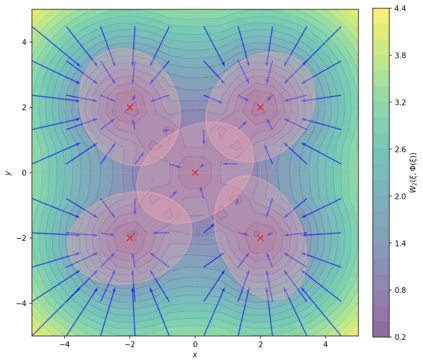
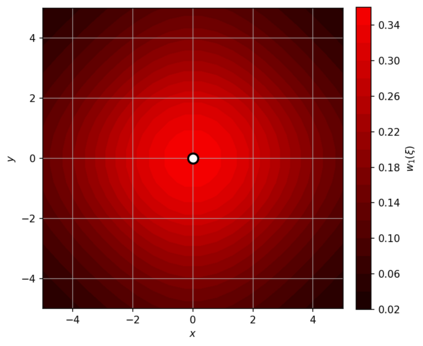
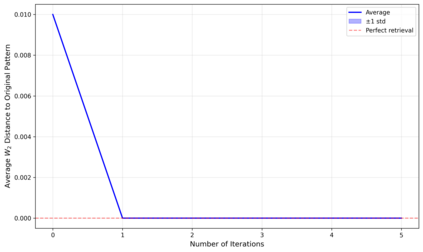
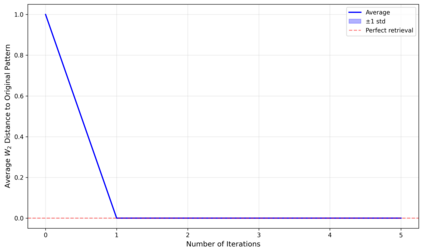
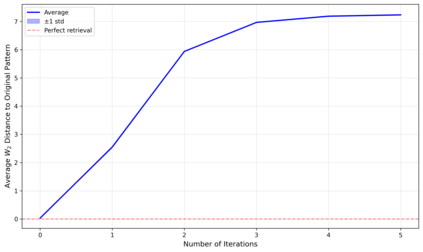
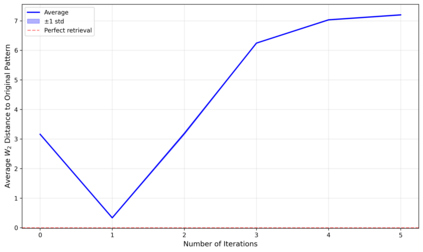
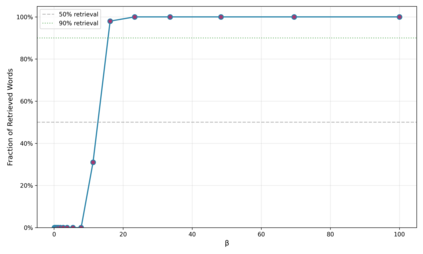
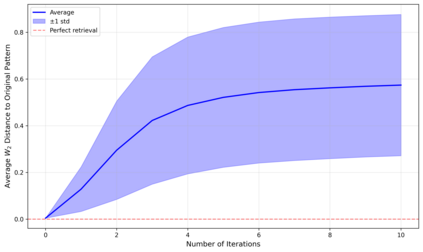
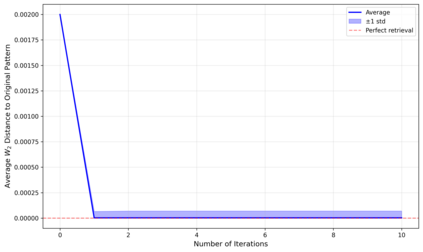
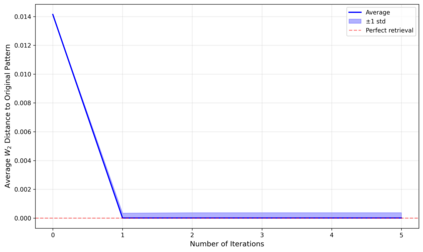
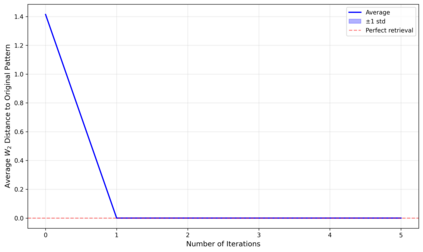
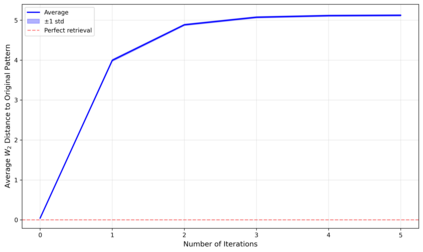
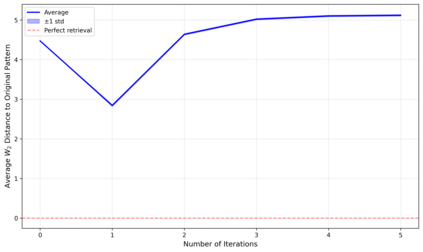
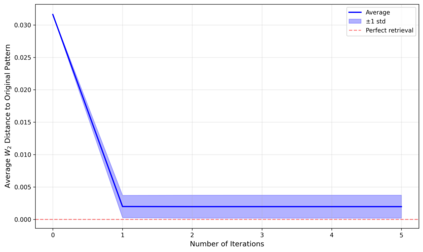
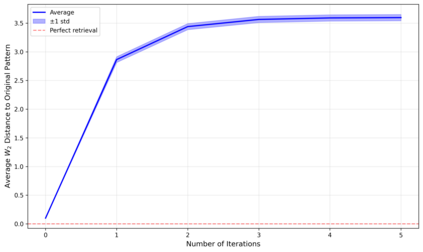
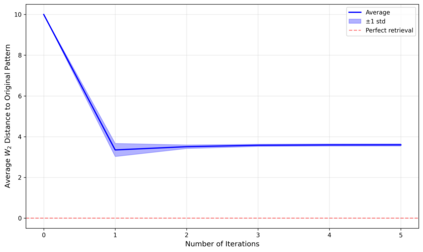
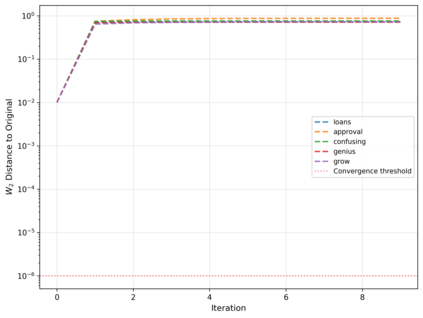
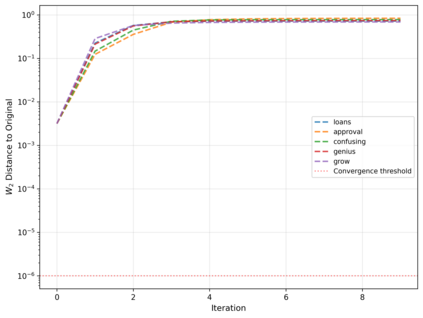
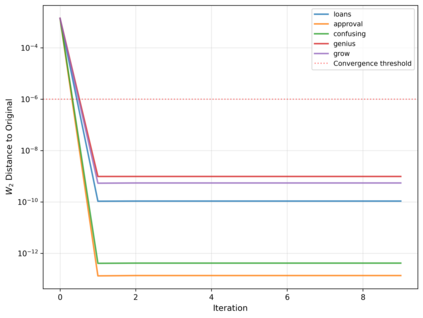
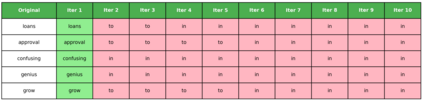
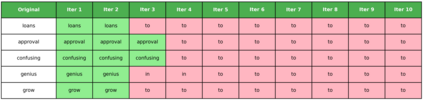
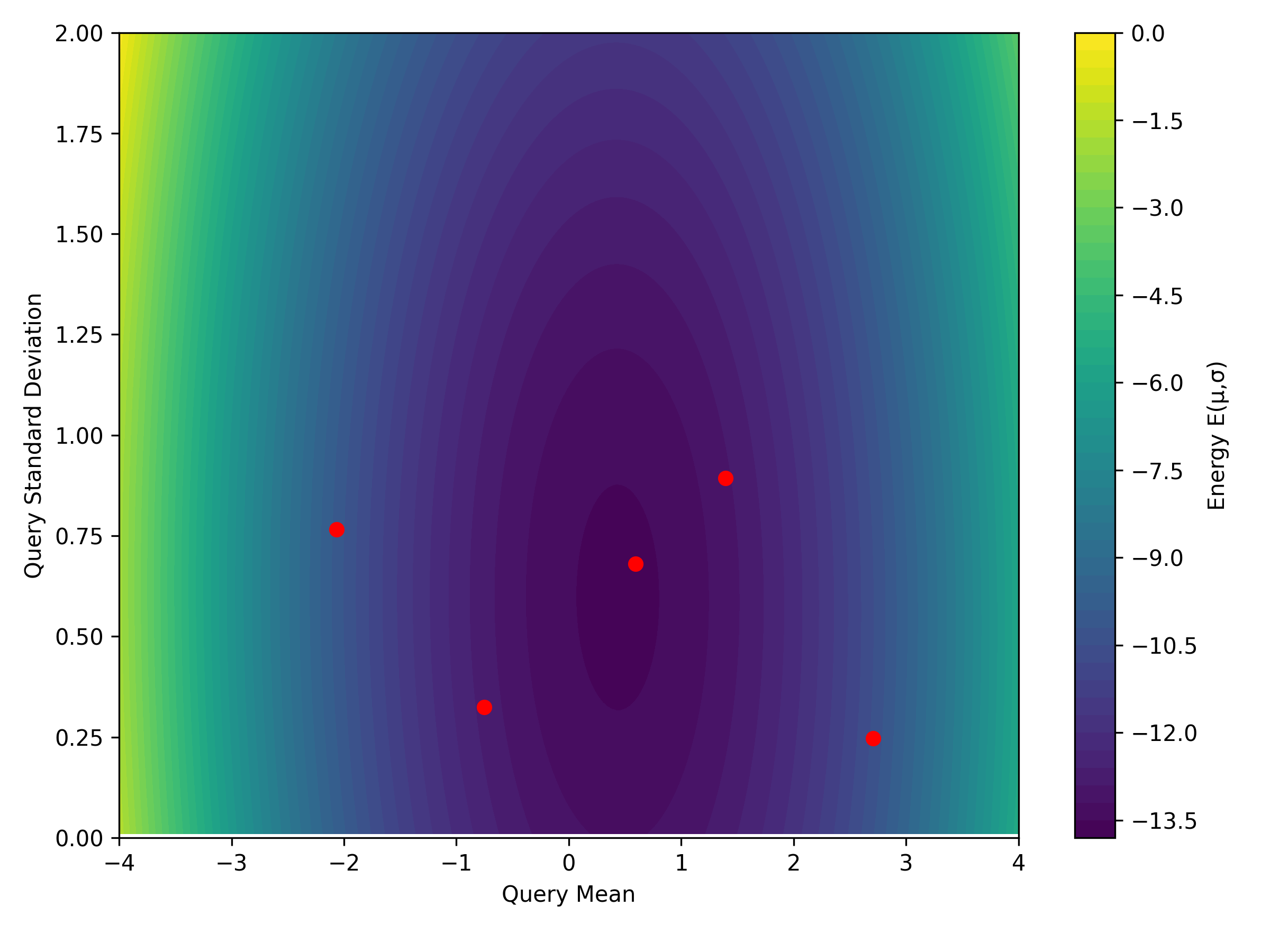
Dense associative memories (DAMs) store and retrieve patterns via energy-functional fixed points, but existing models are limited to vector representations. We extend DAMs to probability distributions equipped with the 2-Wasserstein distance, focusing mainly on the Bures-Wasserstein class of Gaussian densities. Our framework defines a log-sum-exp energy over stored distributions and a retrieval dynamics aggregating optimal transport maps in a Gibbs-weighted manner. Stationary points correspond to self-consistent Wasserstein barycenters, generalizing classical DAM fixed points. We prove exponential storage capacity, provide quantitative retrieval guarantees under Wasserstein perturbations, and validate the model on synthetic and real-world distributional tasks. This work elevates associative memory from vectors to full distributions, bridging classical DAMs with modern generative modeling and enabling distributional storage and retrieval in memory-augmented learning.

翻译：暂无翻译