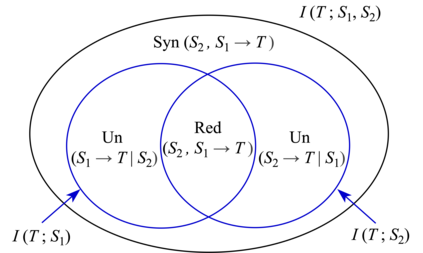
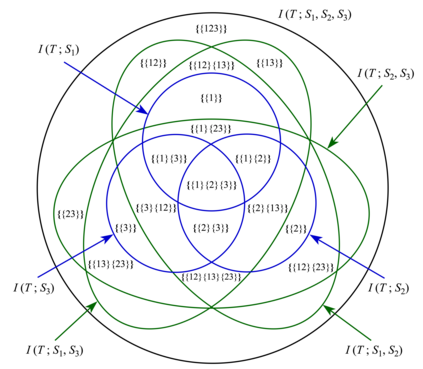
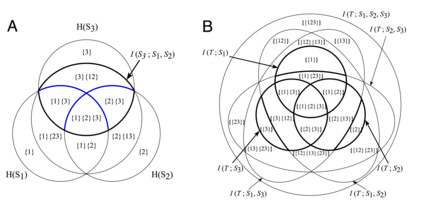
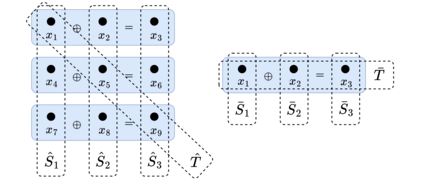
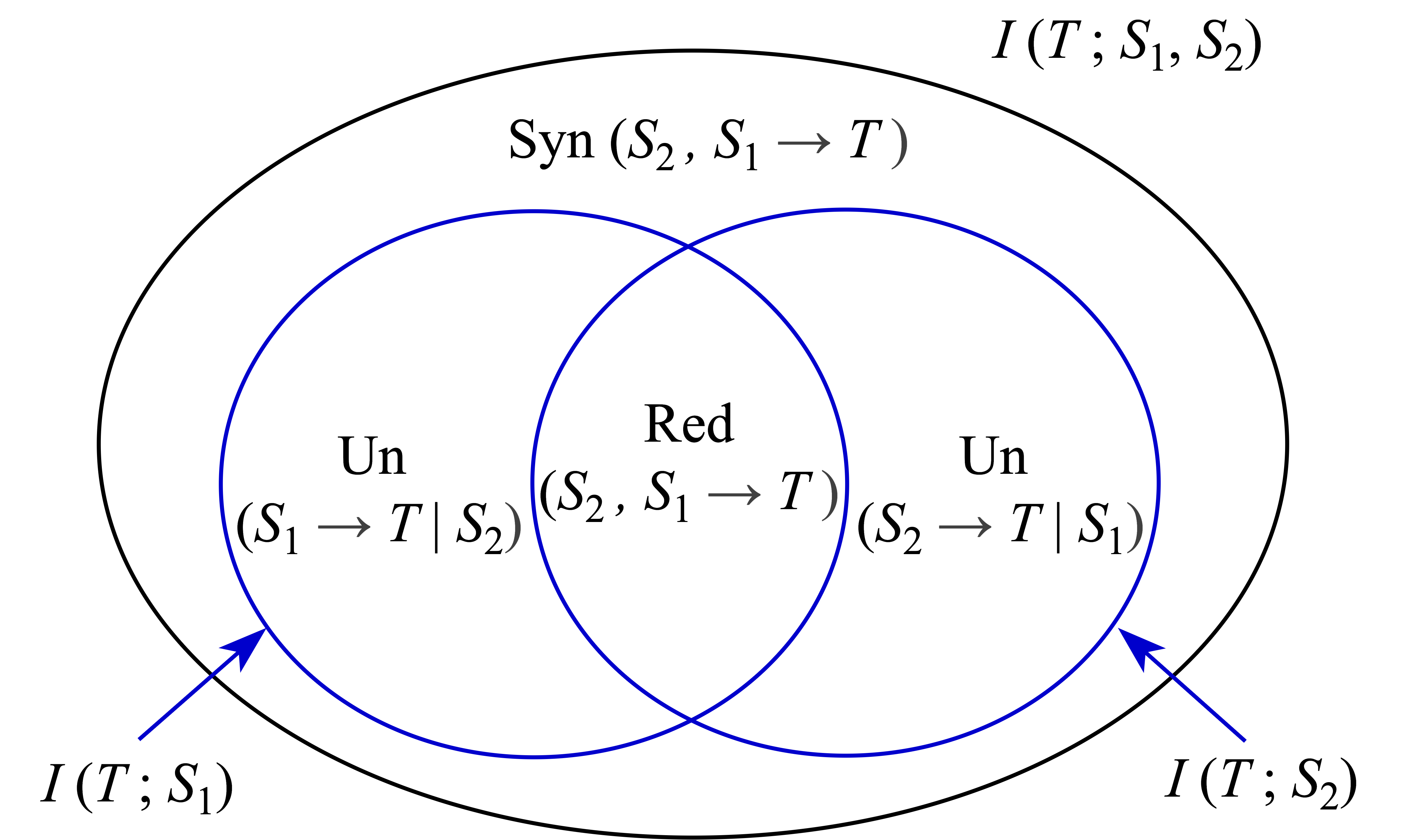
Partial Information Decomposition (PID) was proposed by Williams and Beer in 2010 as a tool for analyzing fine-grained interactions between multiple random variables, and has since found numerous applications ranging from neuroscience to privacy. However, a unified theoretical framework remains elusive due to key conceptual and technical challenges. We identify and illustrate a crucial problem: PID violates the set-theoretic principle that the whole equals the sum of its parts (WESP). Through a counterexample in a three-variable system, we demonstrate how such violations naturally arise, revealing a fundamental limitation of current lattice-based PID frameworks. To address this issue, we introduce a new axiomatic framework, termed System Information Decomposition (SID), specifically tailored for three-variable systems. SID resolves the WESP violation by redefining the summation rules of decomposed information atoms based on synergistic relationships. However, we further show that for systems with four or more variables, no partial summation approach within the existing lattice-based structures can fully eliminate WESP inconsistencies. Our results thus highlight the inherent inadequacy of (antichain) lattice-based decompositions for general multivariate systems.

翻译：暂无翻译