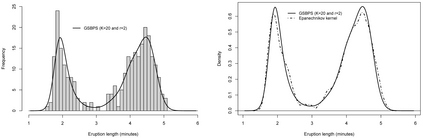
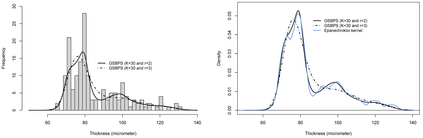
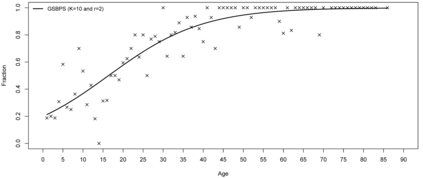
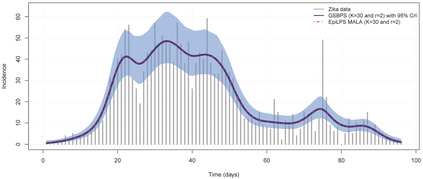
P-splines provide a flexible setting for modeling nonlinear model components based on a discretized penalty structure with a relatively simple computational backbone. Under a Bayesian inferential framework based on Markov chain Monte Carlo, estimates of model coefficients in P-splines models are typically obtained by means of Metropolis-type algorithms. These algorithms rely on a proposal distribution that has to be carefully chosen to generate Markov chains that efficiently explore the parameter space. To avoid such a sensitive tuning choice, we extend the Gibbs sampler to Bayesian P-splines models. In this model class, conditional posterior distributions of model coefficients are shown to have attractive mathematical properties. Taking advantage of these properties, we propose to sample the conditional posteriors by alternating between the adaptive rejection sampler when targets are log-concave and the Griddy-Gibbs sampler when targets are characterized by more complex shapes. The proposed Gibbs sampler for Bayesian P-splines (GSBPS) algorithm is shown to be an interesting tuning-free tool for inference in Bayesian P-splines models. Moreover, the GSBPS algorithm can be translated in a compact and user-friendly routine. After describing theoretical results, we illustrate the potential of our methodology in density estimation, Binomial regression, and smoothing of epidemic curves.

翻译：暂无翻译