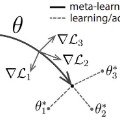
Learning new tasks by drawing on prior experience gathered from other (related) tasks is a core property of any intelligent system. Gradient-based meta-learning, especially MAML and its variants, has emerged as a viable solution to accomplish this goal. One problem MAML encounters is its computational and memory burdens needed to compute the meta-gradients. We propose a new first-order variant of MAML that we prove converges to a stationary point of the MAML objective, unlike other first-order variants. We also show that the MAML objective does not satisfy the smoothness assumption assumed in previous works; we show instead that its smoothness constant grows with the norm of the meta-gradient, which theoretically suggests the use of normalized or clipped-gradient methods compared to the plain gradient method used in previous works. We validate our theory on a synthetic experiment.

翻译：暂无翻译