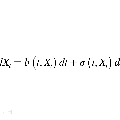Characterizing the differential privacy (DP) of learning algorithms has become a major challenge in recent years. In parallel, many studies suggested investigating the behavior of stochastic gradient descent (SGD) with heavy-tailed noise, both as a model for modern deep learning models and to improve their performance. However, most DP bounds focus on light-tailed noise, where satisfactory guarantees have been obtained but the proposed techniques do not directly extend to the heavy-tailed setting. Recently, the first DP guarantees for heavy-tailed SGD were obtained. These results provide $(0,δ)$-DP guarantees without requiring gradient clipping. Despite casting new light on the link between DP and heavy-tailed algorithms, these results have a strong dependence on the number of parameters and cannot be extended to other DP notions like the well-established Rényi differential privacy (RDP). In this work, we propose to address these limitations by deriving the first RDP guarantees for heavy-tailed SDEs, as well as their discretized counterparts. Our framework is based on new Rényi flow computations and the use of well-established fractional Poincaré inequalities. Under the assumption that such inequalities are satisfied, we obtain DP guarantees that have a much weaker dependence on the dimension compared to prior art.

翻译：刻画学习算法的差分隐私（DP）特性已成为近年来的主要挑战。与此同时，许多研究建议探究带有重尾噪声的随机梯度下降（SGD）行为，这既可作为现代深度学习模型的表征，也有助于提升其性能。然而，现有大多数DP界限主要针对轻尾噪声场景——该场景已获得令人满意的理论保证，但所提出的技术无法直接推广至重尾噪声设定。近期，首次针对重尾SGD的DP保证被提出，这些结果提供了$(0,δ)$-DP保证且无需梯度裁剪。尽管这些成果为DP与重尾算法之间的关联提供了新视角，但其结果对参数数量存在强依赖性，且无法扩展至其他DP概念（如成熟的Rényi差分隐私（RDP））。本研究通过推导重尾随机微分方程及其离散化形式的首个RDP保证，致力于解决上述局限性。我们的理论框架基于新的Rényi流计算与成熟的分数Poincaré不等式应用。在满足此类不等式的前提下，我们获得的DP保证相较于现有成果具有更弱的维度依赖性。