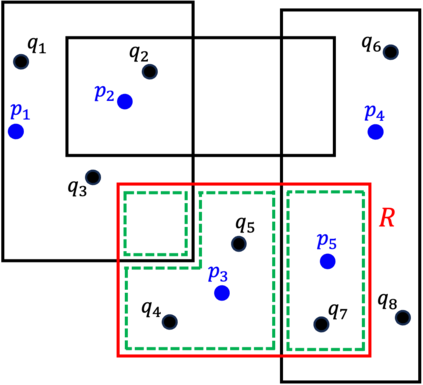
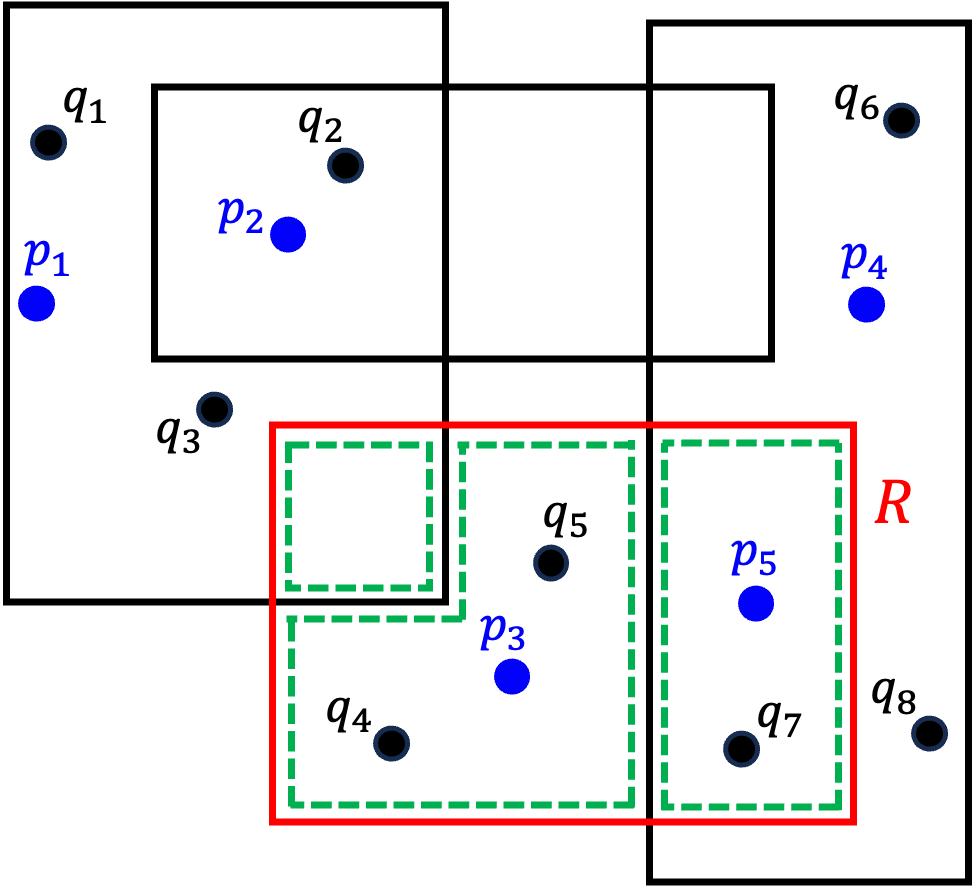
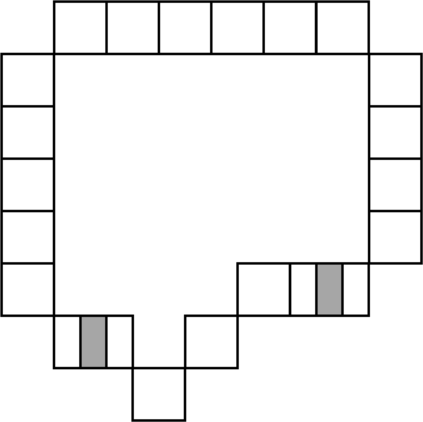We are given a set $\mathcal{Z}=\{(R_1,s_1),\ldots, (R_n,s_n)\}$, where each $R_i$ is a \emph{range} in $\Re^d$, such as rectangle or ball, and $s_i \in [0,1]$ denotes its \emph{selectivity}. The goal is to compute a small-size \emph{discrete data distribution} $\mathcal{D}=\{(q_1,w_1),\ldots, (q_m,w_m)\}$, where $q_j\in \Re^d$ and $w_j\in [0,1]$ for each $1\leq j\leq m$, and $\sum_{1\leq j\leq m}w_j= 1$, such that $\mathcal{D}$ is the most \emph{consistent} with $\mathcal{Z}$, i.e., $\mathrm{err}_p(\mathcal{D},\mathcal{Z})=\frac{1}{n}\sum_{i=1}^n\! \lvert{s_i-\sum_{j=1}^m w_j\cdot 1(q_j\in R_i)}\rvert^p$ is minimized. In a database setting, $\mathcal{Z}$ corresponds to a workload of range queries over some table, together with their observed selectivities (i.e., fraction of tuples returned), and $\mathcal{D}$ can be used as compact model for approximating the data distribution within the table without accessing the underlying contents. In this paper, we obtain both upper and lower bounds for this problem. In particular, we show that the problem of finding the best data distribution from selectivity queries is $\mathsf{NP}$-complete. On the positive side, we describe a Monte Carlo algorithm that constructs, in time $O((n+\delta^{-d})\delta^{-2}\mathop{\mathrm{polylog}})$, a discrete distribution $\tilde{\mathcal{D}}$ of size $O(\delta^{-2})$, such that $\mathrm{err}_p(\tilde{\mathcal{D}},\mathcal{Z})\leq \min_{\mathcal{D}}\mathrm{err}_p(\mathcal{D},\mathcal{Z})+\delta$ (for $p=1,2,\infty$) where the minimum is taken over all discrete distributions. We also establish conditional lower bounds, which strongly indicate the infeasibility of relative approximations as well as removal of the exponential dependency on the dimension for additive approximations. This suggests that significant improvements to our algorithm are unlikely.

翻译：暂无翻译