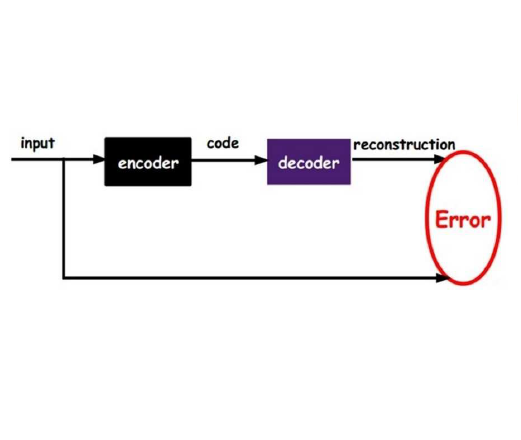
Linear Autoencoders (LAEs) have shown strong performance in state-of-the-art recommender systems. However, this success remains largely empirical, with limited theoretical understanding. In this paper, we investigate the generalizability -- a theoretical measure of model performance in statistical learning -- of multivariate linear regression and LAEs. We first propose a PAC-Bayes bound for multivariate linear regression, extending the earlier bound for single-output linear regression by Shalaeva et al., and establish sufficient conditions for its convergence. We then show that LAEs, when evaluated under a relaxed mean squared error, can be interpreted as constrained multivariate linear regression models on bounded data, to which our bound adapts. Furthermore, we develop theoretical methods to improve the computational efficiency of optimizing the LAE bound, enabling its practical evaluation on large models and real-world datasets. Experimental results demonstrate that our bound is tight and correlates well with practical ranking metrics such as Recall@K and NDCG@K.

翻译：线性自编码器（LAEs）在先进推荐系统中展现出卓越性能，但其成功主要基于实证研究，理论理解仍显不足。本文从统计学习的理论度量——泛化性角度，系统研究了多元线性回归与线性自编码器的理论特性。首先，我们扩展了Shalaeva等人提出的单输出线性回归PAC-Bayes界，构建了多元线性回归的PAC-Bayes界，并建立了其收敛的充分条件。其次，我们证明在松弛均方误差评估下，线性自编码器可解释为有界数据上的约束多元线性回归模型，从而适配本文提出的理论界。进一步，我们发展了优化线性自编码器界的理论方法，提升了计算效率，使其能够在大规模模型和真实数据集上进行实际评估。实验结果表明，该理论界具有紧致性，且与Recall@K、NDCG@K等实际排序指标呈现良好相关性。