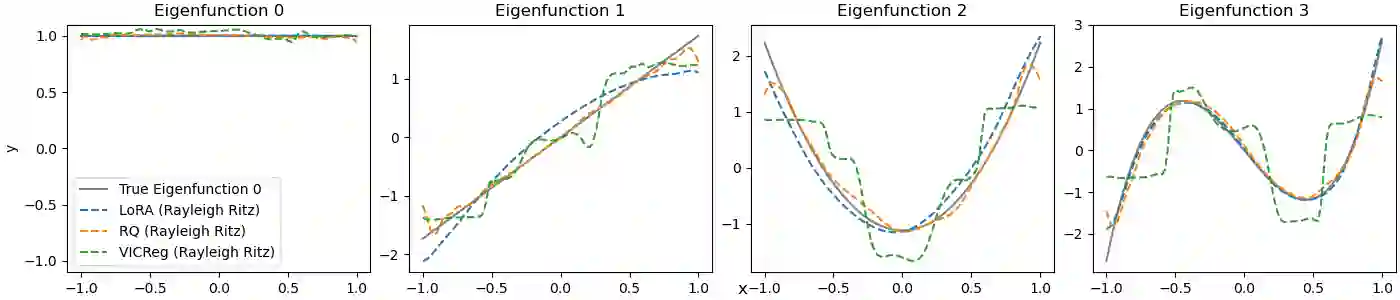
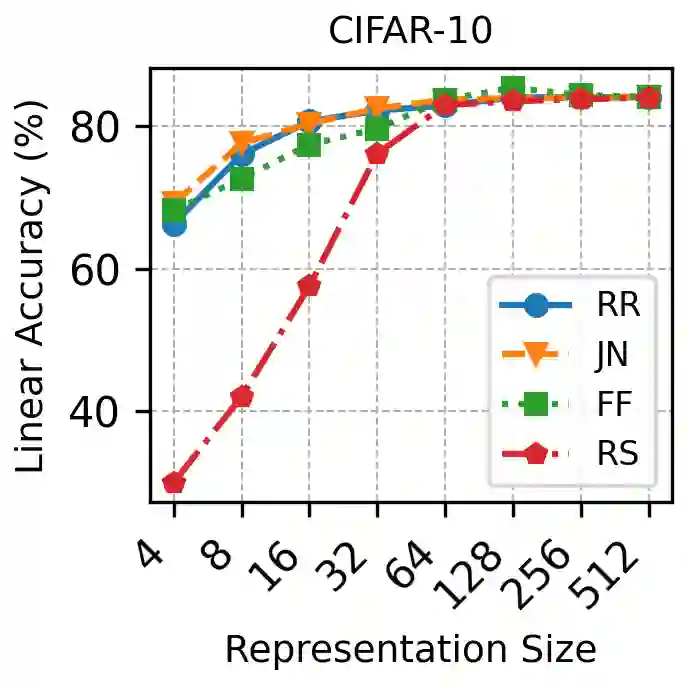
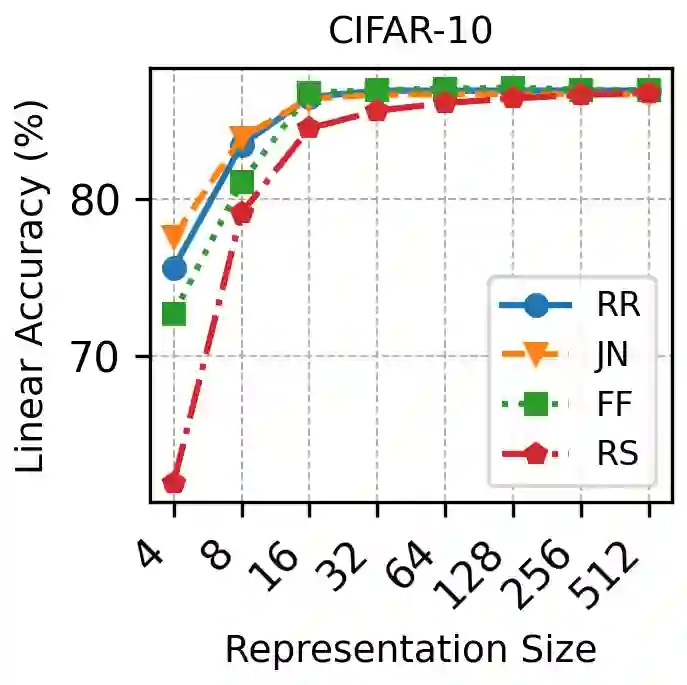
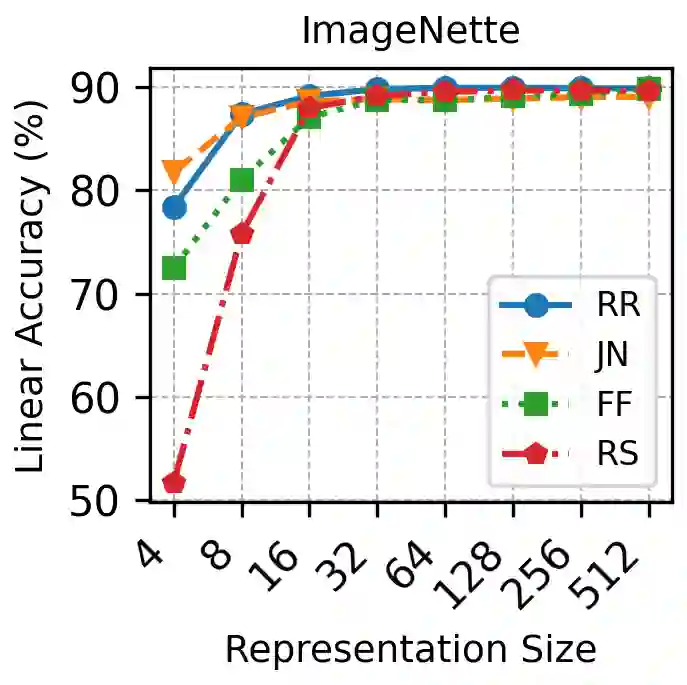
Recent advances in representation learning reveal that widely used objectives, such as contrastive and non-contrastive, implicitly perform spectral decomposition of a contextual kernel, induced by the relationship between inputs and their contexts. Yet, these methods recover only the linear span of top eigenfunctions of the kernel, whereas exact spectral decomposition is essential for understanding feature ordering and importance. In this work, we propose a general framework to extract ordered and identifiable eigenfunctions, based on modular building blocks designed to satisfy key desiderata, including compatibility with the contextual kernel and scalability to modern settings. We then show how two main methodological paradigms, low-rank approximation and Rayleigh quotient optimization, align with this framework for eigenfunction extraction. Finally, we validate our approach on synthetic kernels and demonstrate on real-world image datasets that the recovered eigenvalues act as effective importance scores for feature selection, enabling principled efficiency-accuracy tradeoffs via adaptive-dimensional representations.

翻译：暂无翻译