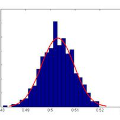
To explore the relationship between dependency distance (DD) and hierarchical distance (HD) in Japanese, we compared the probability distributions of DD and HD with and without sentence length fixed, and analyzed the changes in mean dependency distance (MDD) and mean hierarchical distance (MHD) as sentence length increases, along with their correlation coefficient based on the Balanced Corpus of Contemporary Written Japanese. It was found that the valency of the predicates is the underlying factor behind the trade-off relation between MDD and MHD in Japanese. Native speakers of Japanese regulate the linear complexity and hierarchical complexity through the valency of the predicates, and the relative sizes of MDD and MHD depend on whether the threshold of valency has been reached. Apart from the cognitive load, the valency of the predicates also affects the probability distributions of DD and HD. The effect of the valency of the predicates on the distribution of HD is greater than on that of DD, which leads to differences in their probability distributions and causes the mean of MDD to be lower than that of MHD.

翻译：为探究日语中依存距离（DD）与层级距离（HD）的关系，我们比较了固定句长与非固定句长条件下DD与HD的概率分布，并基于《现代书面日语平衡语料库》分析了平均依存距离（MDD）和平均层级距离（MHD）随句长增加的变化趋势及其相关系数。研究发现，谓词的配价是日语中MDD与MHD权衡关系的根本因素。日语母语者通过谓词配价调控线性复杂度与层级复杂度，MDD与MHD的相对大小取决于是否达到配价阈值。除认知负荷外，谓词配价亦影响DD与HD的概率分布。谓词配价对HD分布的影响大于对DD分布的影响，这导致二者概率分布存在差异，并使MDD的均值低于MHD的均值。