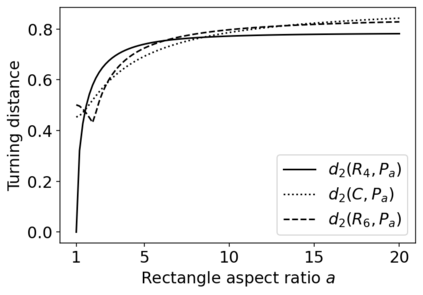
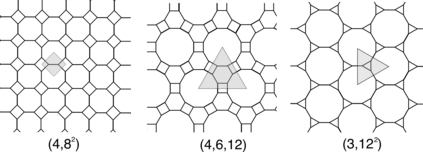
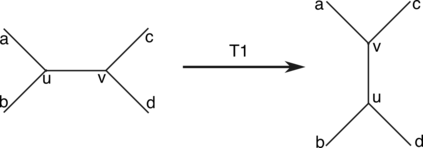
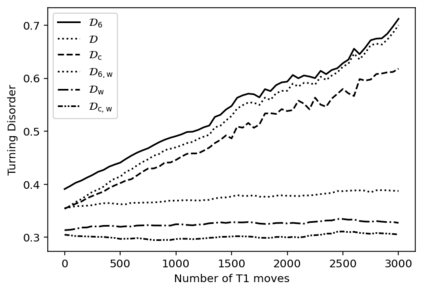
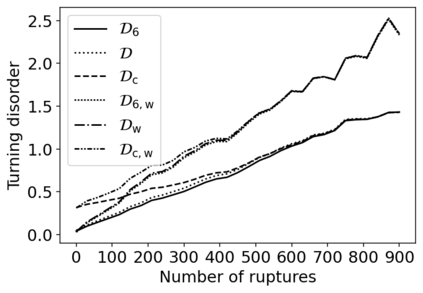
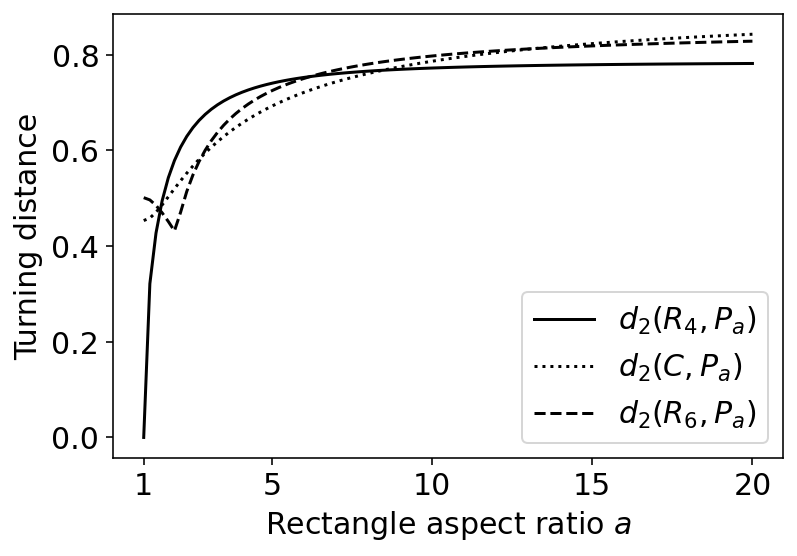
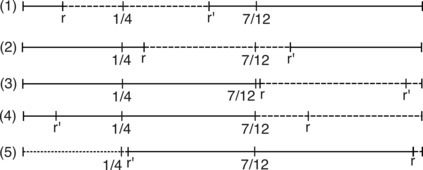The turning distance is a well-studied metric for measuring the similarity between two polygons. This metric is constructed by taking an $L^p$ distance between step functions which track each shape's tangent angle of a path tracing its boundary. In this study, we introduce \textit{turning disorders} for polygonal planar networks, defined by averaging turning distances between network faces and "ordered" shapes (regular polygons or circles). We derive closed-form expressions of turning distances for special classes of regular polygons, related to the divisibility of $m$ and $n$, and also between regular polygons and circles. These formulas are used to show that the time for computing the 2-turning distances reduces to $O((m+n) \log(m+n))$ when both shapes are regular polygons, an improvement from $O(mn\log(mn))$ operations needed to compute distances between general polygons of $n$ and $m$ sides. We also apply these formulas to several examples of network microstructure with varying disorder. For Archimedean lattices, a class of regular tilings, we can express turning disorders with exact expressions. We also consider turning disorders applied to two examples of stochastic processes on networks: spring networks evolving under T1 moves and polygonal rupture processes. We find that the two aspects of defining different turning disorders, the choice of ordered shape and whether to apply area-weighting, can capture different notions of network disorder.

翻译：暂无翻译