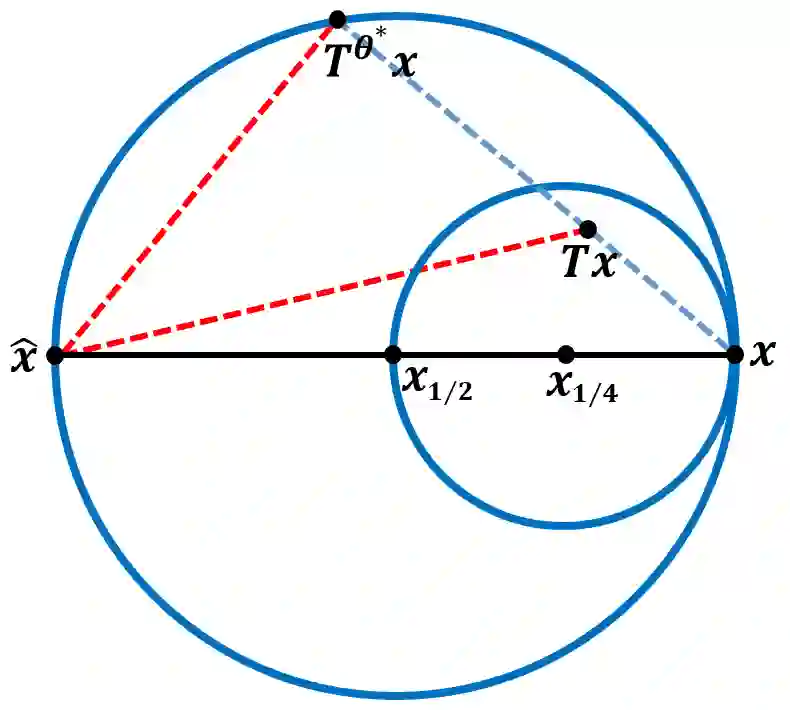
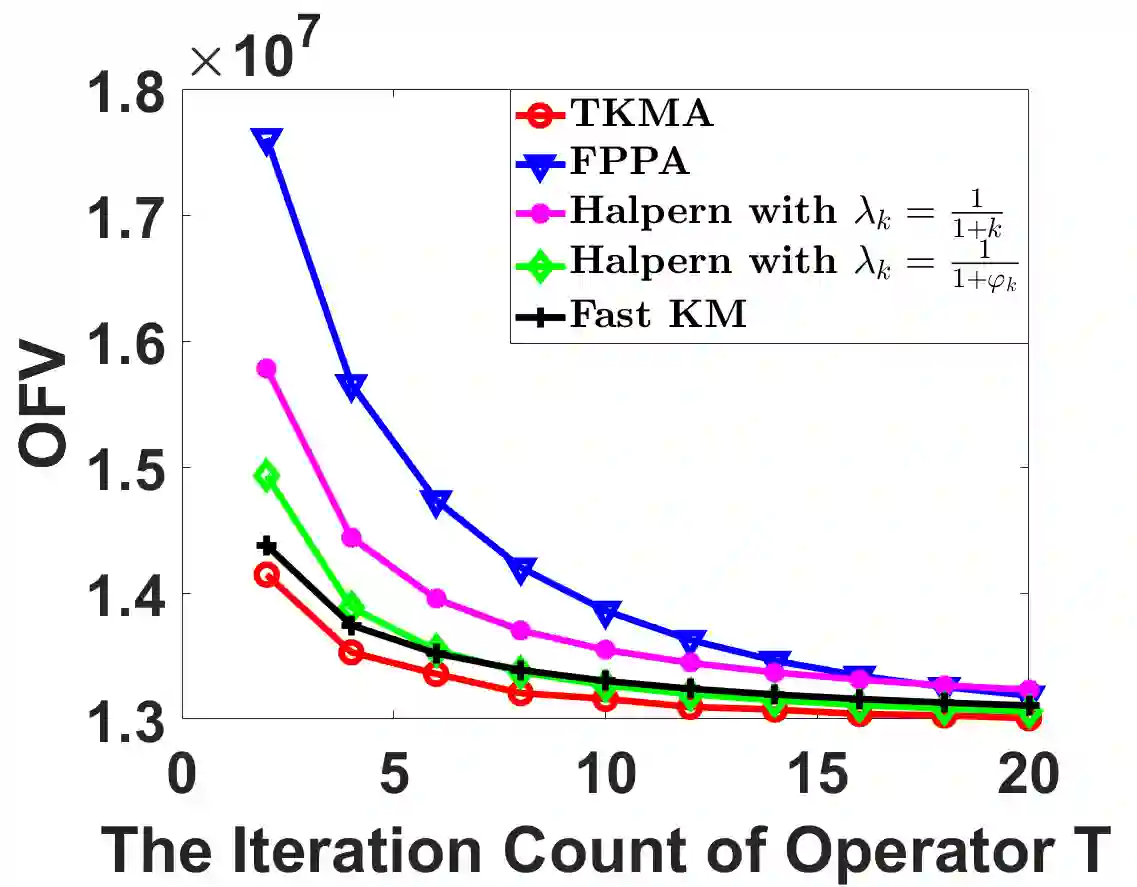
In this paper, we propose a Two-step Krasnosel'skii-Mann (KM) Algorithm (TKMA) with adaptive momentum for solving convex optimization problems arising in image processing. Such optimization problems can often be reformulated as fixed-point problems for certain operators, which are then solved using iterative methods based on the same operator, including the KM iteration, to ultimately obtain the solution to the original optimization problem. Prior to developing TKMA, we first introduce a KM iteration enhanced with adaptive momentum, derived from geometric properties of an averaged nonexpansive operator T, KM acceleration technique, and information from the composite operator T^2. The proposed TKMA is constructed as a convex combination of this adaptive-momentum KM iteration and the Picard iteration of T^2. We establish the convergence of the sequence generated by TKMA to a fixed point of T. Moreover, under specific assumptions on the adaptive momentum parameters, we prove that the algorithm achieves an o(1/k^{1/2}) convergence rate in terms of the distance between successive iterates. Numerical experiments demonstrate that TKMA outperforms the FPPA, PGA, Fast KM algorithm, and Halpern algorithm on tasks such as image denoising and low-rank matrix completion.

翻译：本文提出了一种具有自适应动量的两步Krasnosel'skii-Mann（KM）算法（TKMA），用于解决图像处理中出现的凸优化问题。此类优化问题通常可重构为特定算子的不动点问题，随后采用基于该算子的迭代方法（包括KM迭代）进行求解，最终获得原始优化问题的解。在构建TKMA之前，我们首先引入一种基于自适应动量增强的KM迭代，该迭代源于平均非扩张算子T的几何性质、KM加速技术以及复合算子T^2的信息。所提出的TKMA被构造为此自适应动量KM迭代与T^2的Picard迭代的凸组合。我们证明了TKMA生成的序列收敛于T的不动点。此外，在自适应动量参数满足特定假设的条件下，我们证明了该算法在连续迭代点间距离方面达到o(1/k^{1/2})的收敛速率。数值实验表明，在图像去噪和低秩矩阵补全等任务中，TKMA的性能优于FPPA、PGA、快速KM算法及Halpern算法。