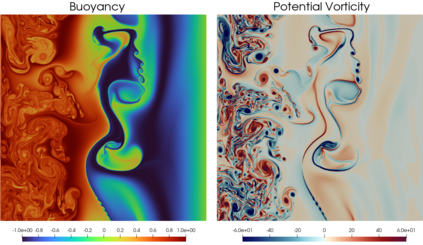
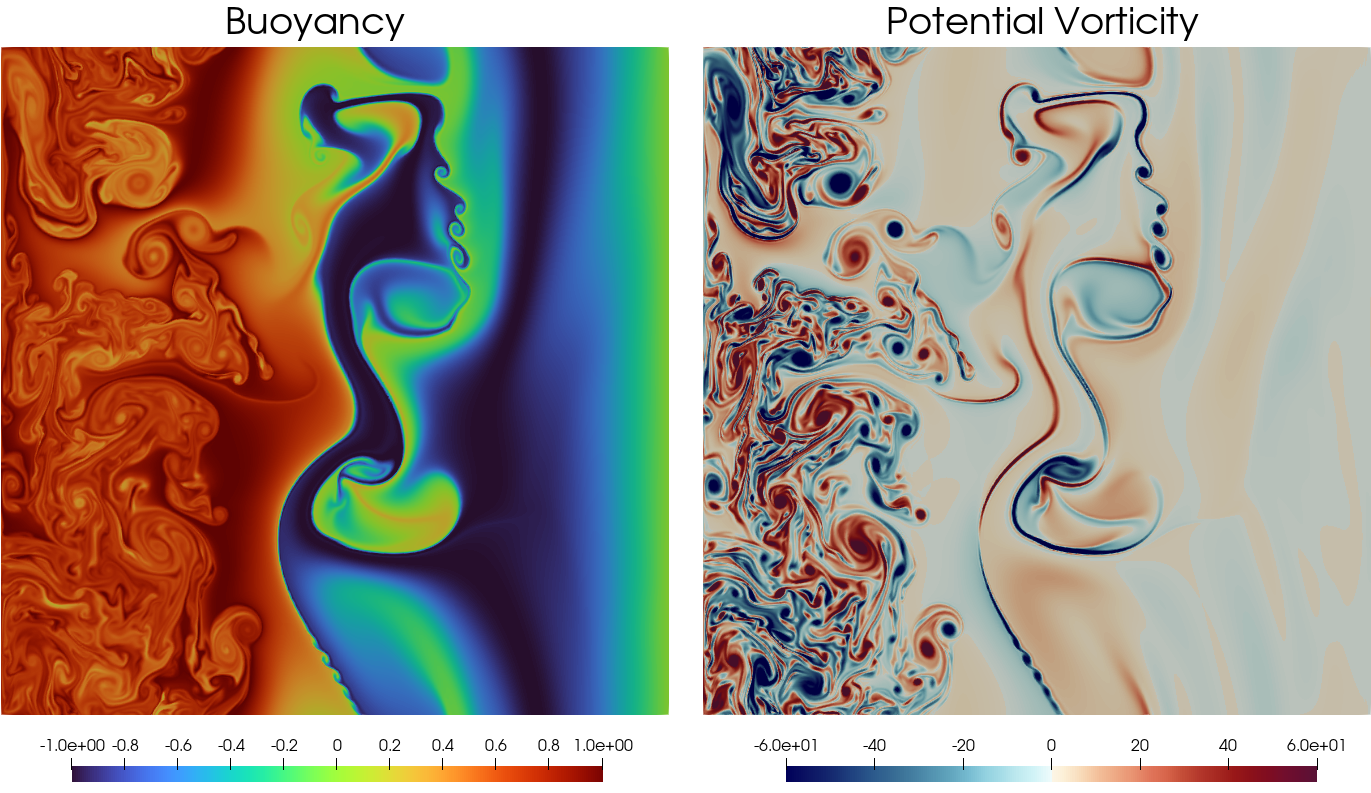
This paper investigates the mathematical properties of a stochastic version of the balanced 2D thermal quasigeostrophic (TQG) model of potential vorticity dynamics. This stochastic TQG model is intended as a basis for parametrisation of the dynamical creation of unresolved degrees of freedom in computational simulations of upper ocean dynamics when horizontal buoyancy gradients and bathymetry affect the dynamics, particularly at the submesoscale (250m-10km). Specifically, we have chosen the SALT (Stochastic Advection by Lie Transport) algorithm introduced in [25] and applied in [11,12] as our modelling approach. The SALT approach preserves the Kelvin circulation theorem and an infinite family of integral conservation laws for TQG. The goal of the SALT algorithm is to quantify the uncertainty in the process of up-scaling, or coarse-graining of either observed or synthetic data at fine scales, for use in computational simulations at coarser scales. The present work provides a rigorous mathematical analysis of the solution properties of the thermal quasigeostrophic (TQG) equations with stochastic advection by Lie transport (SALT) [27,28].

翻译：本文调查了平衡的 2D 热准地球营养(TQG) 模型的数学性质。 这种随机 TQG 模型旨在作为在横向浮度梯度和水深测量影响动态时,在高海洋动态的计算模拟中动态产生未解决的自由度,当横向浮度梯度和测深影响动态时,特别是在亚气象尺度(250米-10公里)时,在高洋动态的计算模拟中,在高洋动态模拟中,特别是在低气象尺度(250米-10公里)时,将平衡的 2D 热准准地球营养(TQQG ) 模型模型的数学特性作为我们的模型方法。 SALT 方法保存了凯尔文循环的理论和TQG 整体保护法的无限组合。 SALT 算法的目标是量化在微尺度上观测到的或合成数据的不确定性,以便在粗尺度上用于计算模拟。 目前的工作对热准地球营养度(TQG) 运输(TQQQG) 等式的热准系统(TQG) 等变压分析提供了严格的数学分析。