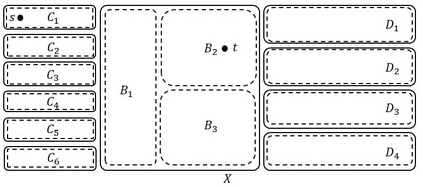
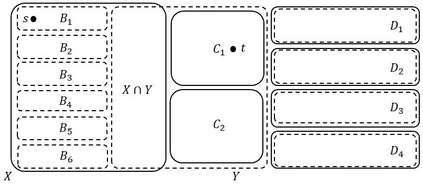
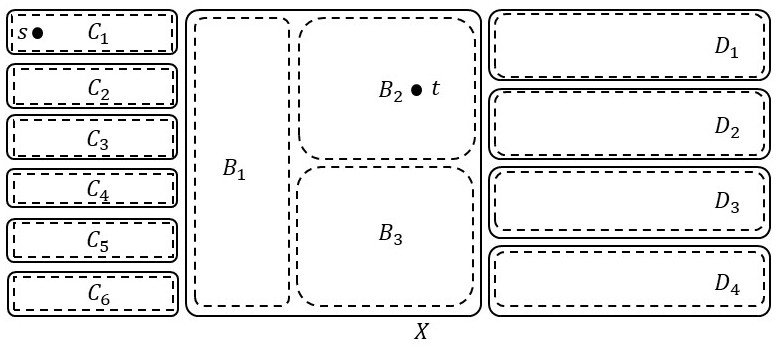
Narayanan and Fujishige showed the existence of the principal partition sequence of a submodular function, a structure with numerous applications in areas such as clustering, fast algorithms, and approximation algorithms. In this work, motivated by two applications, we develop a theory of $\{s,t\}$-separating principal partition sequence of a submodular function. We define this sequence, show its existence, and design a polynomial-time algorithm to construct it. We show two applications: (1) approximation algorithm for the $\{s,t\}$-separating submodular $k$-partitioning problem for monotone and posimodular functions and (2) polynomial-time algorithm for the hypergraph orientation problem of finding an orientation that simultaneously has strong connectivity at least $k$ and $(s,t)$-connectivity at least $\ell$.

翻译：暂无翻译