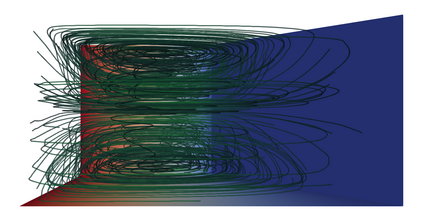
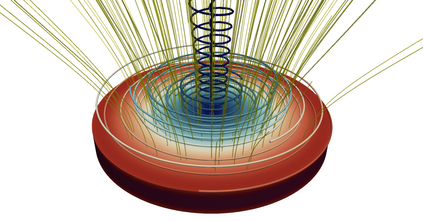
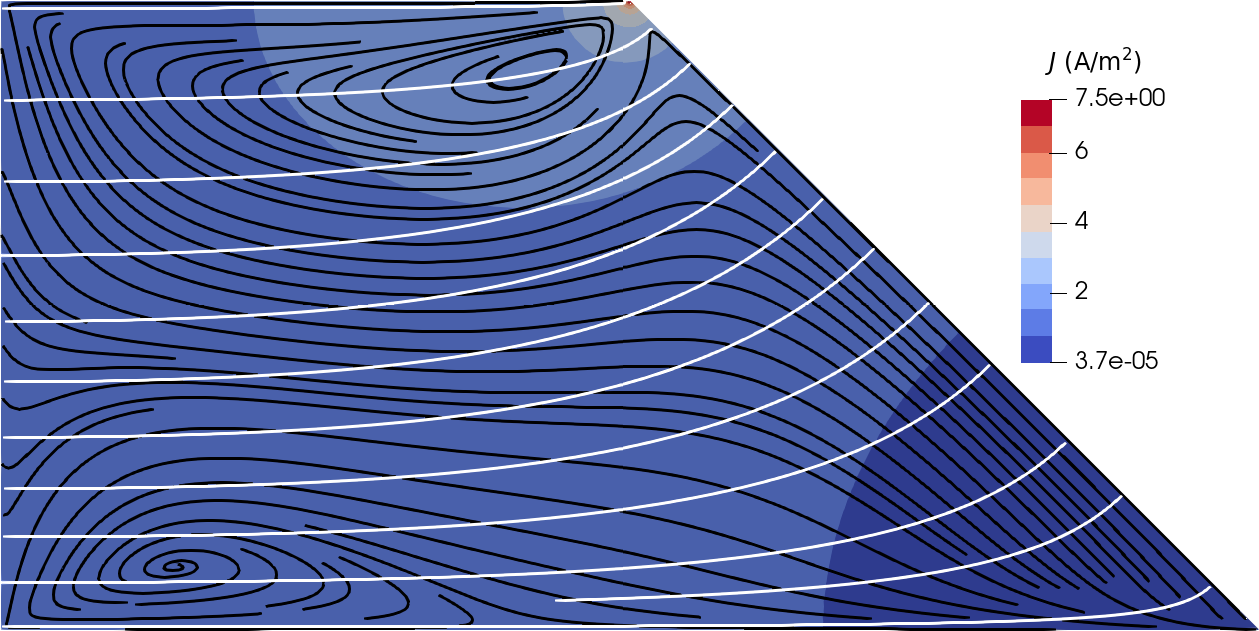
We present a broad family of high-order finite element algorithms for simulating the flow of electroneutral electrolytes. The governing partial differential equations that we solve are the electroneutral Navier-Stokes-Onsager-Stefan-Maxwell (NSOSM) equations, which model momentum transport, multicomponent diffusion and electrical effects within the electrolyte. Our algorithms can be applied in the steady and transient settings, in two and three spatial dimensions, and under a variety of boundary conditions. Moreover, we allow for the material parameters (e.g. viscosity, diffusivities, thermodynamic factors and density) to be solution-dependent and thermodynamically non-ideal. The flexibility of our approach requires us to address subtleties that arise in the governing equations due to the interplay between boundary conditions and the equation of state. We demonstrate the algorithms in various physical configurations, including (i) electrolyte flow around a microfluidic rotating disk electrode and (ii) the flow in a Hull cell of a cosolvent electrolyte mixture used in lithium-ion batteries.

翻译：暂无翻译