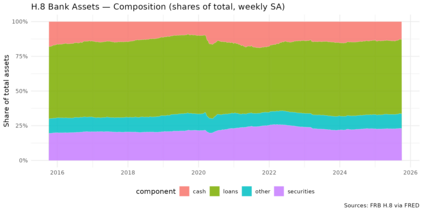
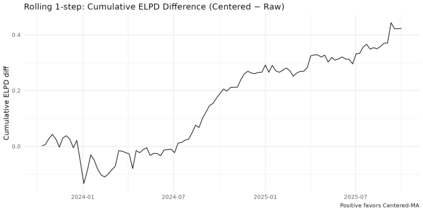
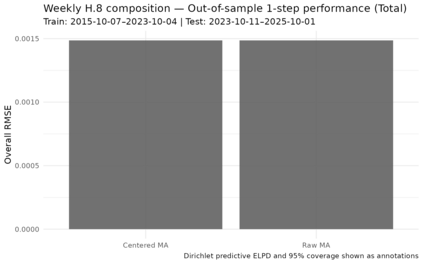
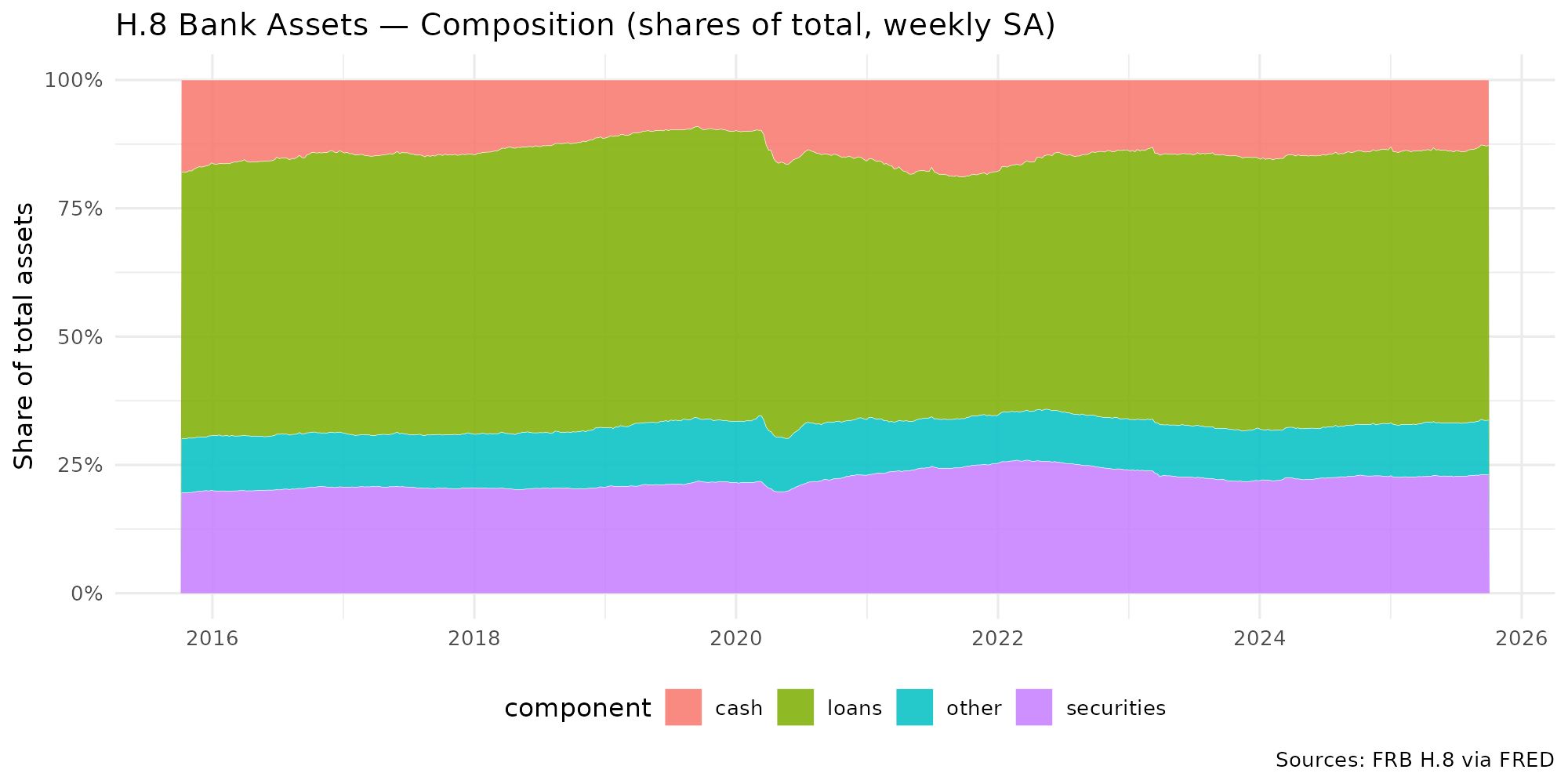
Observation-driven Dirichlet models for compositional time series commonly use the additive log-ratio (ALR) link and include a moving-average (MA) term based on ALR residuals. In the standard Bayesian Dirichlet Auto-Regressive Moving-Average (B-DARMA) recursion, this MA regressor has a nonzero conditional mean under the Dirichlet likelihood, which biases the mean path and complicates interpretation of the MA coefficients. We propose a minimal change: replace the raw regressor with a centered innovation equal to the ALR residual minus its conditional expectation, computable in closed form using digamma functions. Centering restores mean-zero innovations for the MA block without altering either the likelihood or the ALR link. We provide closed-form identities for the conditional mean and forecast recursion, show first-order equivalence to a digamma-link DARMA while retaining a simple inverse back to the mean composition, and supply ready-to-use code. In a weekly application to the Federal Reserve H.8 bank-asset composition, the centered specification improves log predictive scores with virtually identical point accuracy and markedly cleaner Hamiltonian Monte Carlo diagnostics.

翻译：暂无翻译