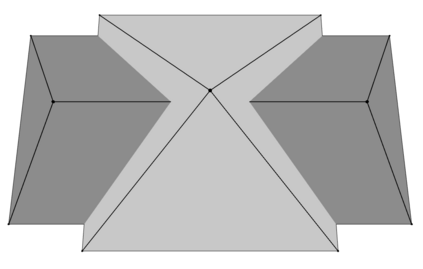
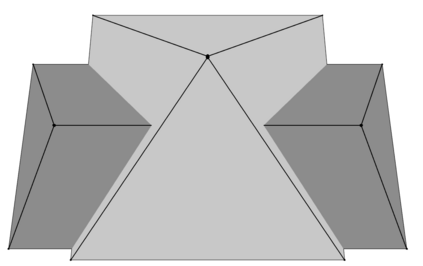
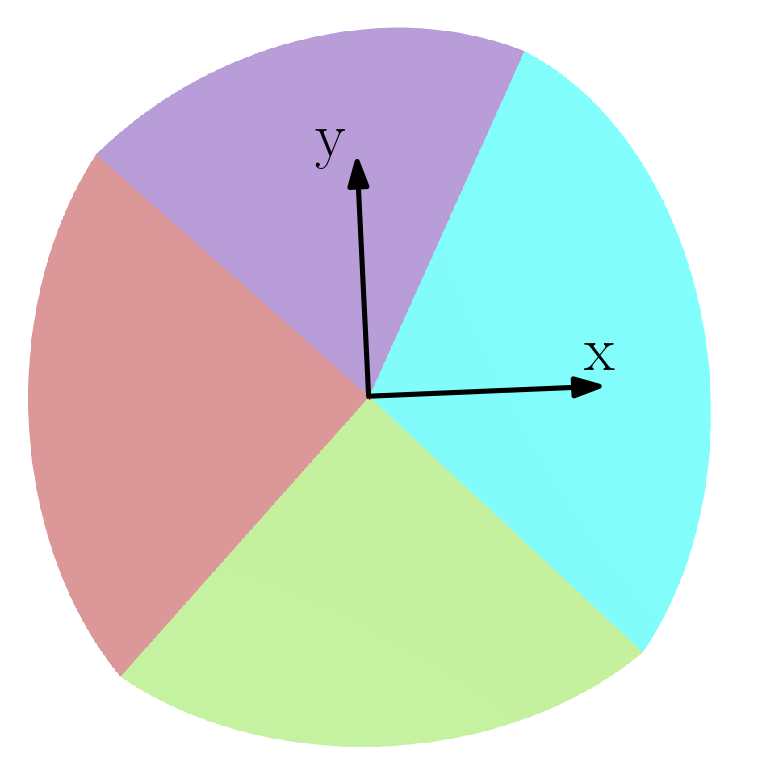
We consider the task of reconstructing polytopes with fixed facet directions from finitely many support function evaluations. We show that for a fixed simplicial normal fan the least-squares estimate is given by a convex quadratic program. We study the geometry of the solution set and give a combinatorial characterization for the uniqueness of the reconstruction in this case. We provide an algorithm that, under mild assumptions, converges to the unknown input shape as the number of noisy support function evaluations increases. We also discuss limitations of our results if the restriction on the normal fan is removed.

翻译：我们从有限的许多支持功能评价中考虑用固定面部方向重建多端顶楼的任务。 我们显示,对于固定的简易正常扇子来说,最小平方的估计数是由一个二次曲线程序提供的。 我们研究所设定的解决方案的几何学,并对本案中重建的独特性进行组合性定性。 我们提供了一种算法,根据温和的假设,随着噪音支持功能评价数量的增加,这种算法会与未知的输入形状汇合。 我们还讨论如果取消对正常扇子的限制,结果的局限性。