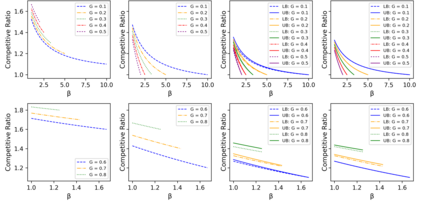
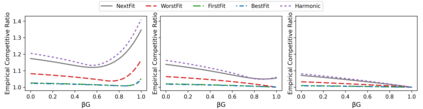
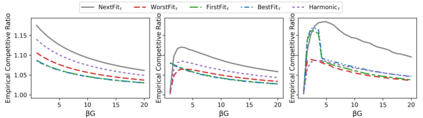
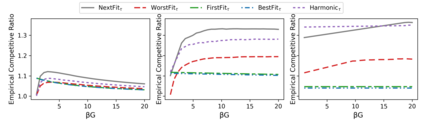
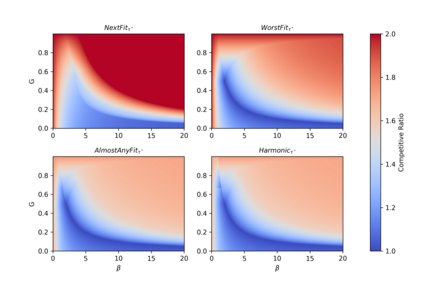
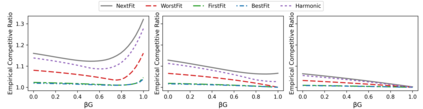
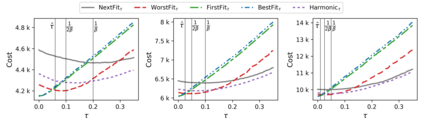
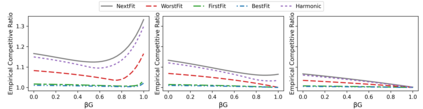
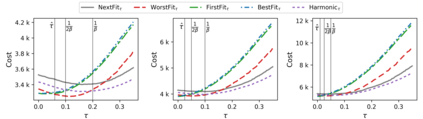
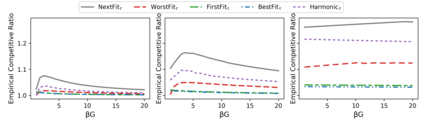
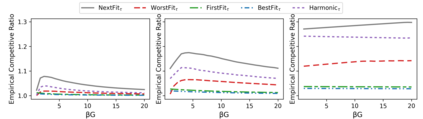
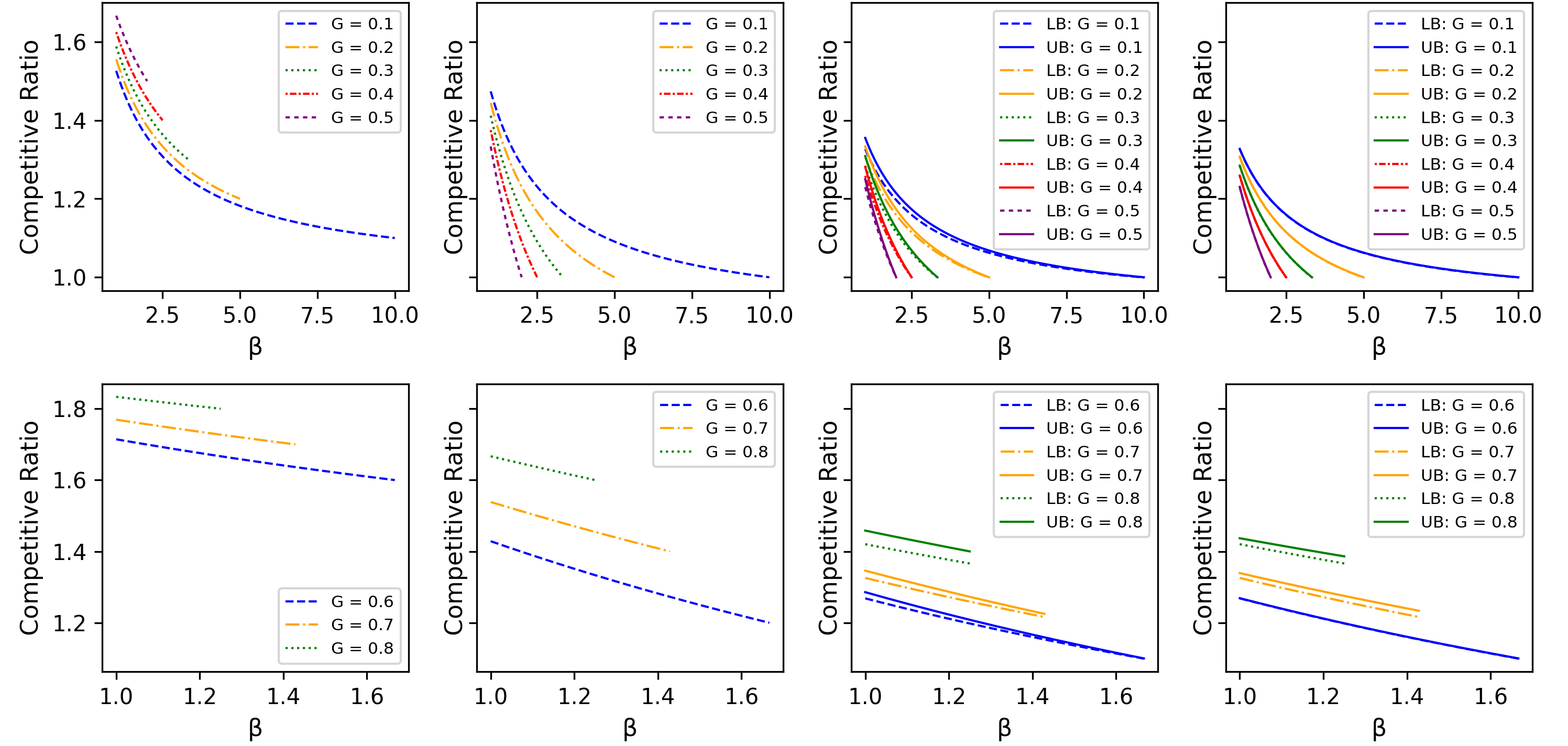
The online bin packing problem and its variants are regularly used to model server allocation problems. Modern concerns surrounding sustainability and overcommitment in cloud computing motivate bin packing models that capture costs associated with highly utilized servers. In this work, we introduce the green bin packing problem, an online variant with a linear cost $\beta$ for filling above a fixed level $G$. For a given instance, the goal is to minimize the sum of the number of opened bins and the linear cost. We show that when $\beta G \le 1$, classical online bin packing algorithms such as FirstFit or Harmonic perform well, and can achieve competitive ratios lower than in the classic setting. However, when $\beta G > 1$, new algorithmic solutions can improve both worst-case and typical performance. We introduce variants of classic online bin packing algorithms and establish theoretical bounds, as well as test their empirical performance.

翻译：暂无翻译