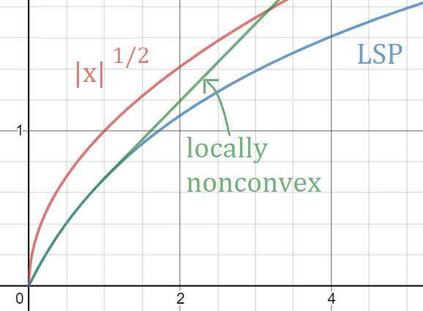
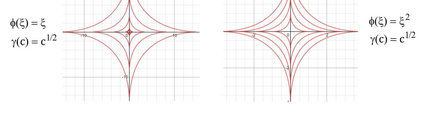
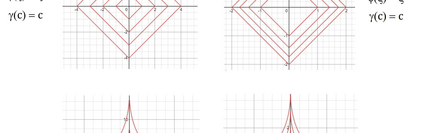
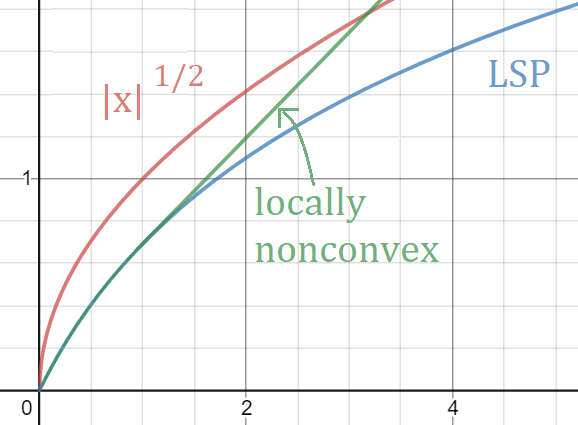
The conditional gradient method (CGM) is widely used in large-scale sparse convex optimization, having a low per iteration computational cost for structured sparse regularizers and a greedy approach to collecting nonzeros. We explore the sparsity acquiring properties of a general penalized CGM (P-CGM) for convex regularizers and a reweighted penalized CGM (RP-CGM) for nonconvex regularizers, replacing the usual convex constraints with gauge-inspired penalties. This generalization does not increase the per-iteration complexity noticeably. Without assuming bounded iterates or using line search, we show $O(1/t)$ convergence of the gap of each subproblem, which measures distance to a stationary point. We couple this with a screening rule which is safe in the convex case, converging to the true support at a rate $O(1/(\delta^2))$ where $\delta \geq 0$ measures how close the problem is to degeneracy. In the nonconvex case the screening rule converges to the true support in a finite number of iterations, but is not necessarily safe in the intermediate iterates. In our experiments, we verify the consistency of the method and adjust the aggressiveness of the screening rule by tuning the concavity of the regularizer.

翻译：有条件的梯度法(CGM)被广泛用于大规模稀疏的混凝土优化,对于结构性稀疏的正规化者来说,每迭代计算成本较低,而对于收集非零度则采用贪婪的方法。我们探索的是,对于混凝土的正规化者来说,获得普遍受罚的CGM(P-CGM)特性的宽度,对于非混凝土的正规化者来说,则获得重新加权的受罚的CGM(RP-CGM)特性的宽度,用受测量激励的罚款取代通常的康氏限制。这种普遍化不会明显增加每升一次的复杂度。在不承担受约束的迭代或使用线搜索的情况下,我们显示每个子问题的差距(1美元/t)的趋近于一个固定点。我们把它与一个在混凝固的案例中很安全的筛选规则结合起来,在一种按 $O(1/(\) delta) 和geq 0. 0. 美元 衡量问题是如何接近解问题的精确性。在非凝固性的情况下, 筛选规则与我们定期的精确性测试的精确性 。