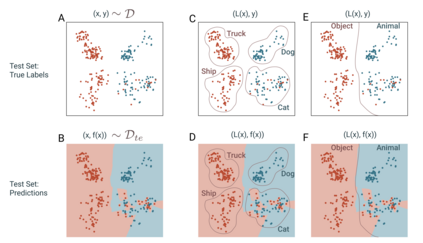
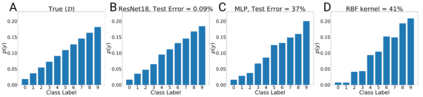
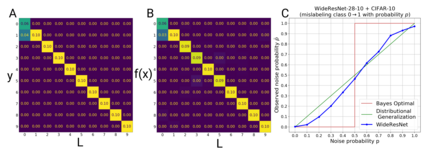
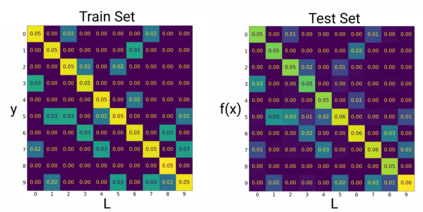
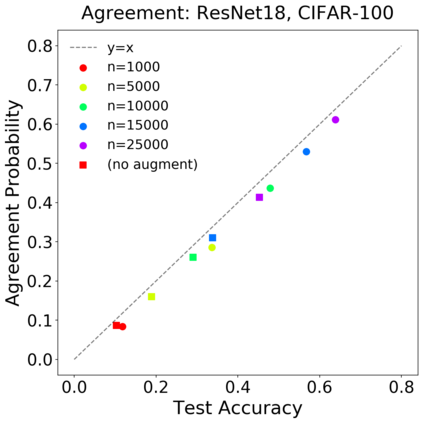
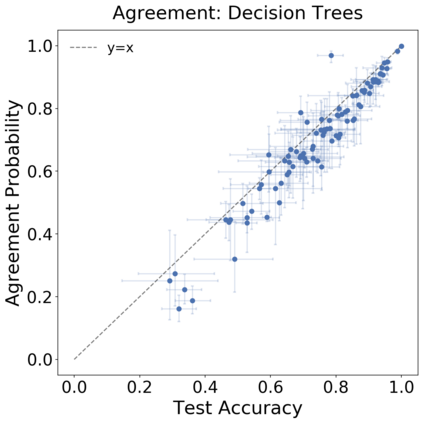
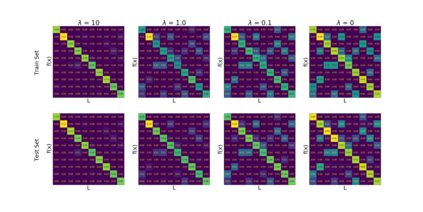
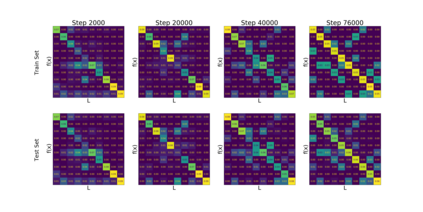
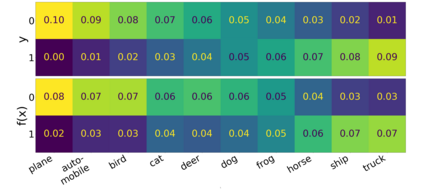
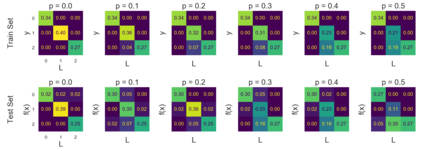
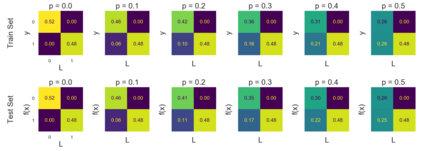
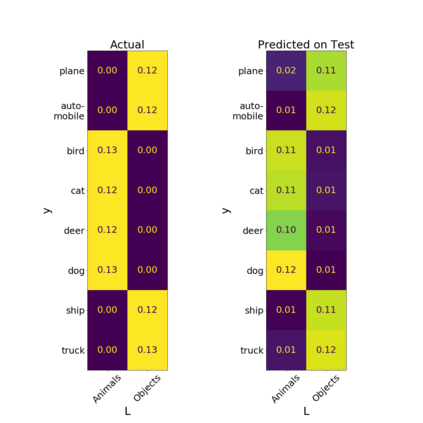
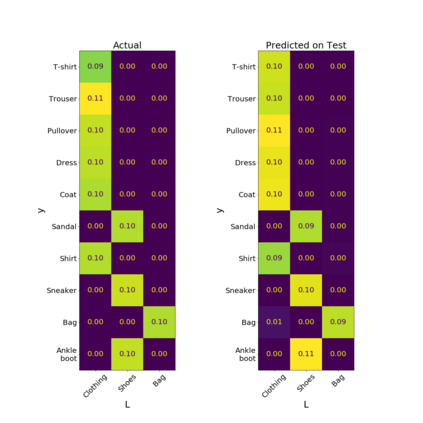
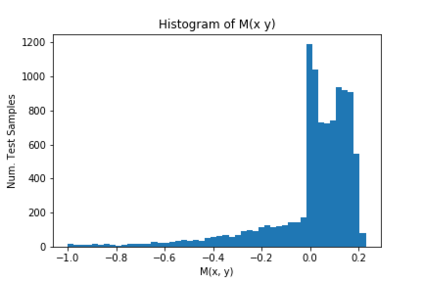
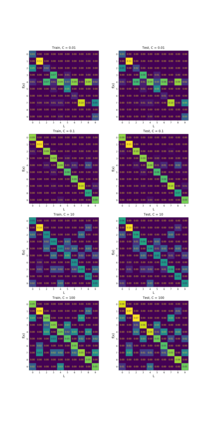
We introduce a new notion of generalization -- Distributional Generalization -- which roughly states that outputs of a classifier at train and test time are close *as distributions*, as opposed to close in just their average error. For example, if we mislabel 30% of dogs as cats in the train set of CIFAR-10, then a ResNet trained to interpolation will in fact mislabel roughly 30% of dogs as cats on the *test set* as well, while leaving other classes unaffected. This behavior is not captured by classical generalization, which would only consider the average error and not the distribution of errors over the input domain. Our formal conjectures, which are much more general than this example, characterize the form of distributional generalization that can be expected in terms of problem parameters: model architecture, training procedure, number of samples, and data distribution. We give empirical evidence for these conjectures across a variety of domains in machine learning, including neural networks, kernel machines, and decision trees. Our results thus advance our empirical understanding of interpolating classifiers.

翻译：我们引入了一种新的一般化概念 -- -- 分布式概括化 -- -- 大致上说列车和测试时间的分类师的输出接近 *as 分布*,而不是平均差错。例如,如果我们在CIFAR-10的列车中误将30%的狗标为猫,那么受过内插训练的ResNet实际上会误将大约30%的狗标为猫,同时使其他类别不受影响。这种行为没有被传统的概括化所捕捉,它只会考虑到输入域的平均差错而不是差错的分布。我们的正式预测,比这个例子更为一般得多,是按问题参数(模型结构、培训程序、样品数量和数据分布)来预期的分布式概括化的形式。我们为机器学习的各个领域,包括神经网络、内核机和决策树等,提供了这些推测的经验证据。我们的结果因此提高了我们对内插分类师的经验理解。