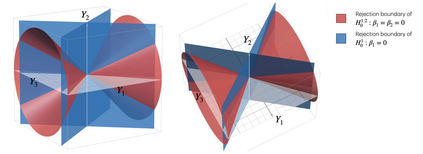
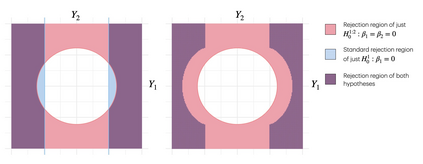
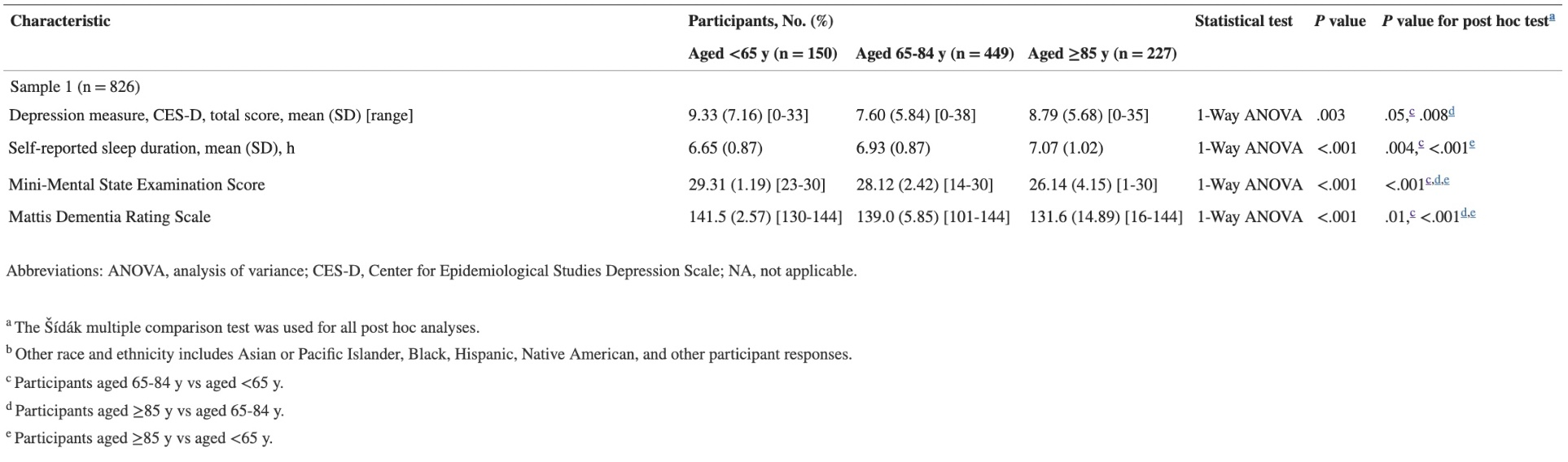
Suppose that a data analyst wishes to report the results of a least squares linear regression only if the overall null hypothesis, $H_0^{1:p}: \beta_1= \beta_2 = \ldots = \beta_p=0$, is rejected. This practice, which we refer to as F-screening (since the overall null hypothesis is typically tested using an $F$-statistic), is in fact common practice across a number of applied fields. Unfortunately, it poses a problem: standard guarantees for the inferential outputs of linear regression, such as Type 1 error control of hypothesis tests and nominal coverage of confidence intervals, hold unconditionally, but fail to hold conditional on rejection of the overall null hypothesis. In this paper, we develop an inferential toolbox for the coefficients in a least squares model that are valid conditional on rejection of the overall null hypothesis. We develop selective p-values that lead to tests that are consistent and control the selective Type 1 error, i.e., the Type 1 error conditional on having rejected the overall null hypothesis. Furthermore, they can be computed without access to the raw data, i.e., using only the standard outputs of a least squares linear regression, and therefore are suitable for use in a retrospective analysis of a published study. We also develop confidence intervals that attain nominal selective coverage, and point estimates that account for having rejected the overall null hypothesis. We derive an expression for the Fisher information about the coefficients resulting from the proposed approach, and compare this to the Fisher information that results from an alternative approach that relies on sample splitting. We investigate the proposed approach in simulation and via re-analysis of two datasets from the biomedical literature.

翻译：暂无翻译