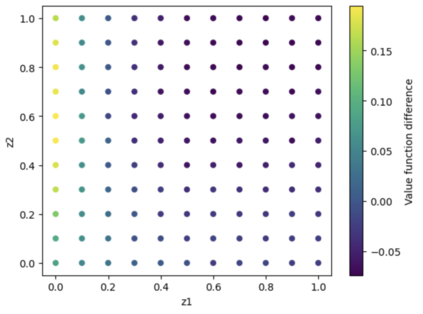
Motivated by applications to the dynamic control of queueing networks, we develop a simulation-based scheme, the so-called multilevel Picard (MLP) approximation, for solving high-dimensional drift control problems whose states are constrained to stay within the nonnegative orthant, over a finite time horizon. We prove that under suitable conditions, the MLP approximation overcomes the curse of dimensionality in the following sense: To approximate the value function and its gradient evaluated at a given time and state to within a prescribed accuracy $\varepsilon$, the computational complexity grows at most polynomially in the problem dimension $d$ and $1/\varepsilon$. To illustrate the effectiveness of the scheme, we carry out numerical experiments for a class of test problems that are related to the dynamic scheduling problem of parallel server systems in heavy traffic, and demonstrate that the scheme is computationally feasible up to dimension at least $20$.

翻译：暂无翻译