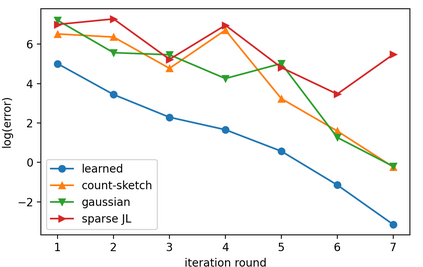
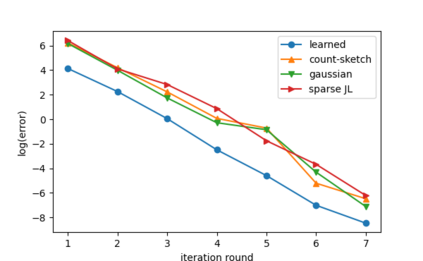
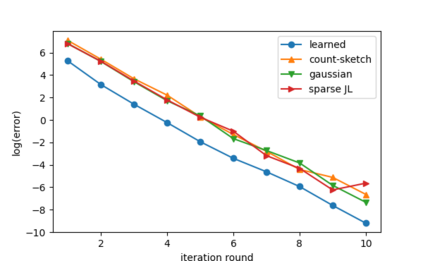
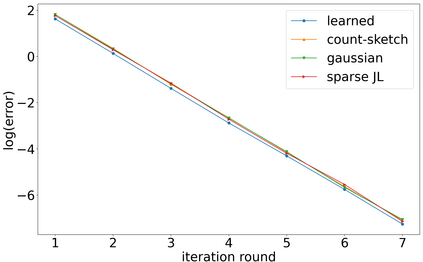
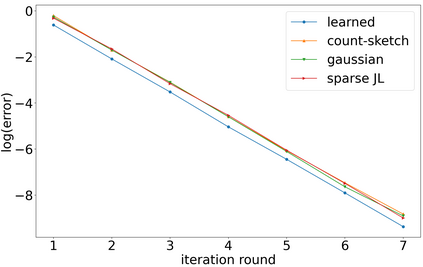
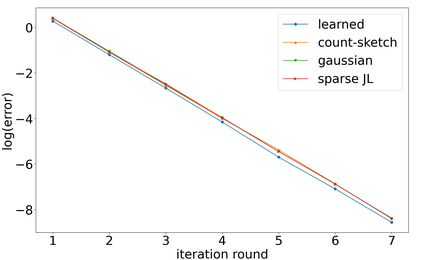
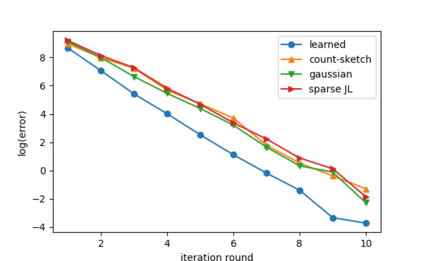
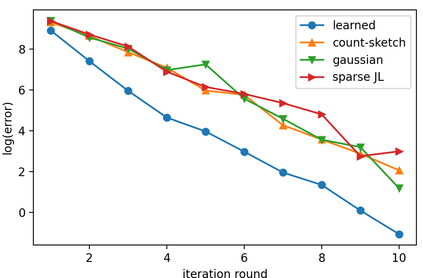
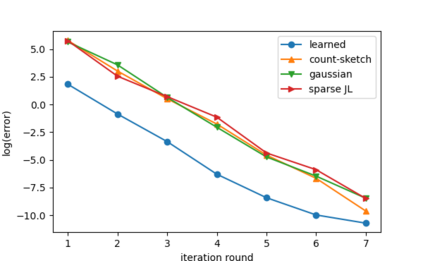
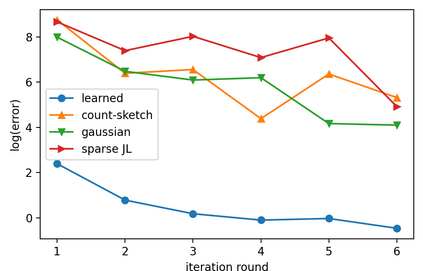
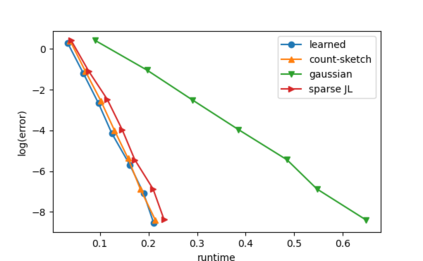
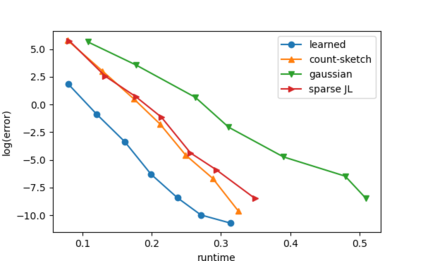
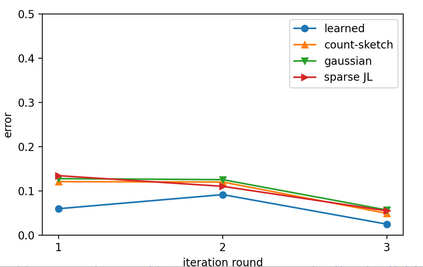
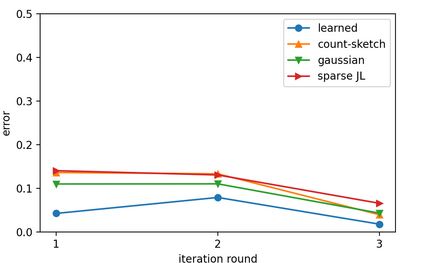
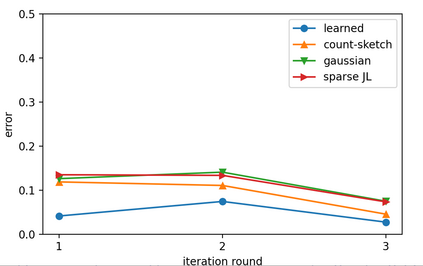
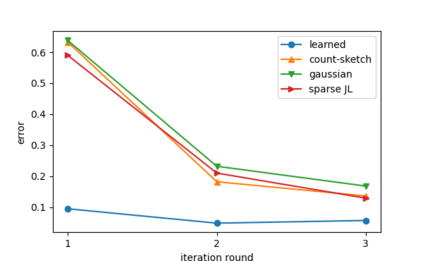
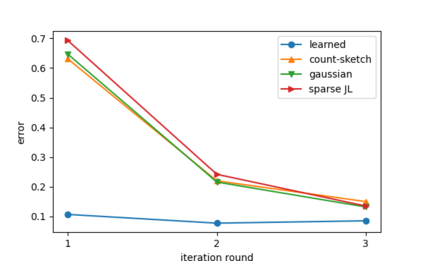
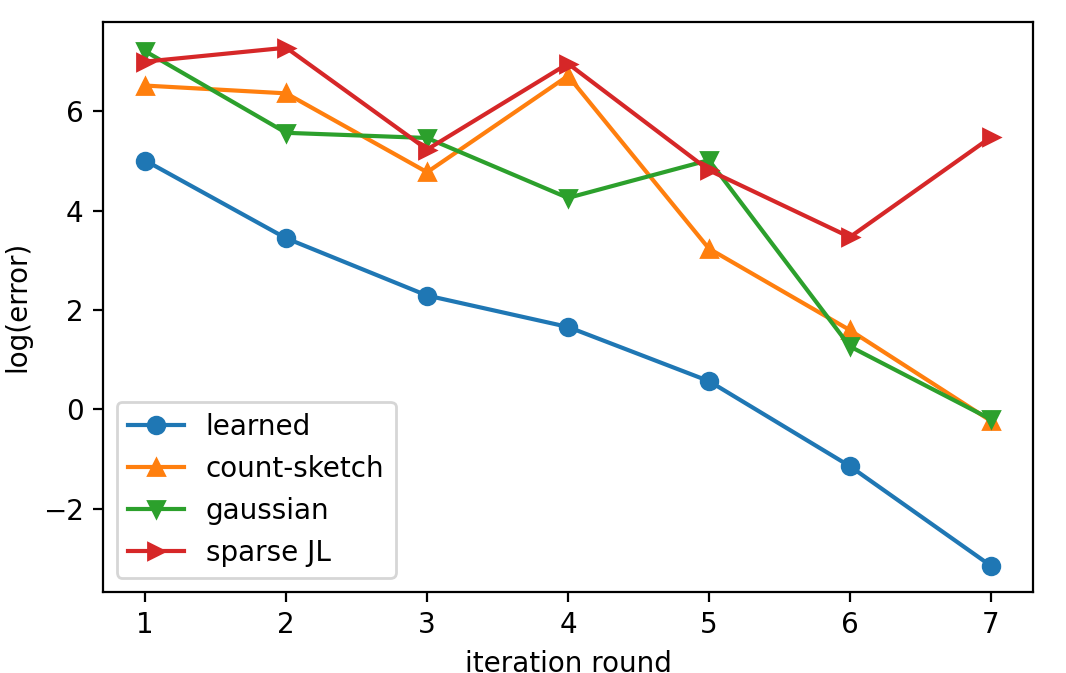
Sketching is a dimensionality reduction technique where one compresses a matrix by linear combinations that are typically chosen at random. A line of work has shown how to sketch the Hessian to speed up each iteration in a second order method, but such sketches usually depend only on the matrix at hand, and in a number of cases are even oblivious to the input matrix. One could instead hope to learn a distribution on sketching matrices that is optimized for the specific distribution of input matrices. We show how to design learned sketches for the Hessian in the context of second order methods, where we learn potentially different sketches for the different iterations of an optimization procedure. We show empirically that learned sketches, compared with their "non-learned" counterparts, improve the approximation accuracy for important problems, including LASSO, SVM, and matrix estimation with nuclear norm constraints. Several of our schemes can be proven to perform no worse than their unlearned counterparts. Additionally, we show that a smaller sketching dimension of the column space of a tall matrix is possible, assuming an oracle for predicting rows which have a large leverage score.

翻译：解剖是一种维度减少技术, 一个人通过一般随机选择的线性组合压缩一个矩阵。 一行工作展示了如何用第二顺序方法绘制赫森人草图以加速每个迭代速度, 但这种草图通常只依赖手头的矩阵, 在很多情况下甚至忽略了输入矩阵。 相反, 人们可能希望学习关于草图矩阵的分布, 以优化的方式分配输入矩阵的具体分布。 我们展示了如何在第二顺序方法中为赫森人设计所学的草图, 我们在那里学习了可能不同的优化程序不同迭代的草图。 我们从经验上显示, 所学的草图与其“ 非学”对应方相比, 提高了重要问题的近似精度, 包括LASSO、 SVM 和有核规范限制的矩阵估测。 我们的一些计划可以证明, 其表现的并不比不吸取数据矩阵的对应方更差。 此外, 我们显示, 高矩阵的柱体空间的细的草图尺寸是可能的, 假设了预测具有较大杠杆的行。