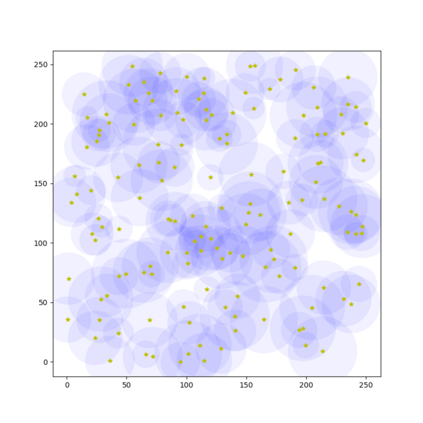
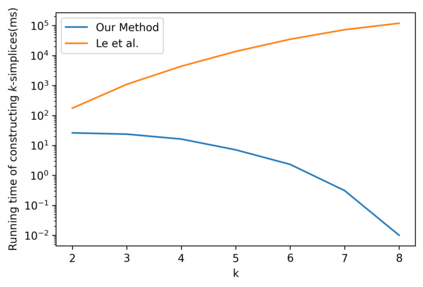
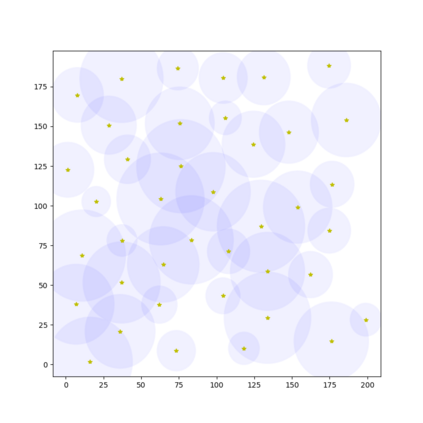
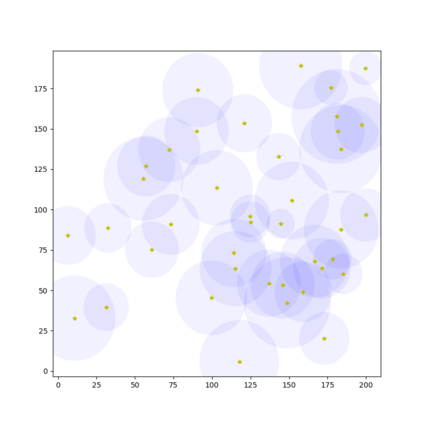
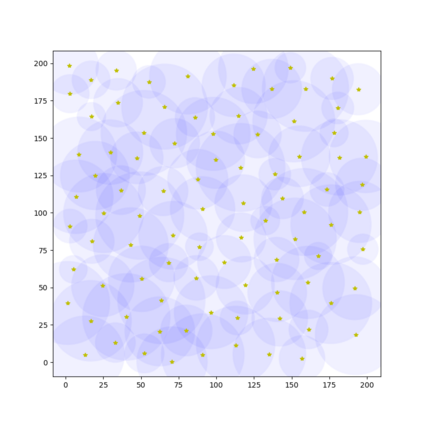
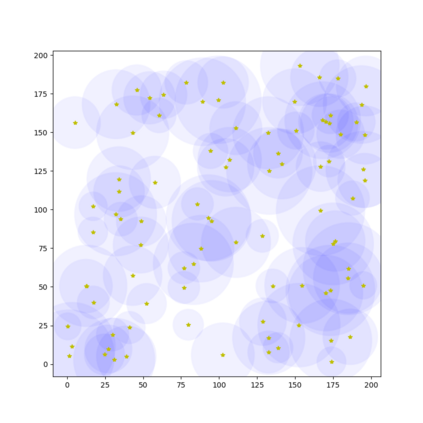
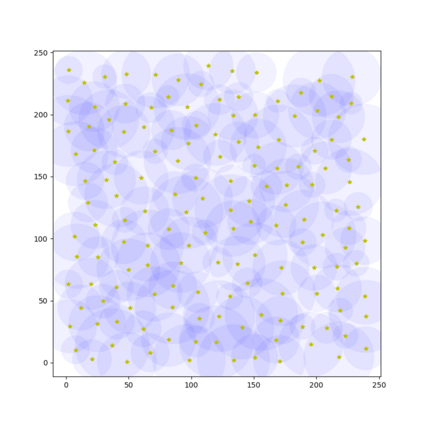
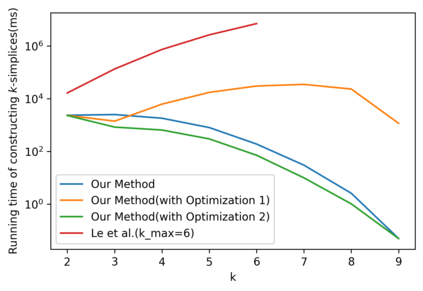
In this paper, we present an algorithm that computes the generalized \v{C}ech complex for a finite set of disks where each may have a different radius in 2D space. An extension of this algorithm is also proposed for a set of balls in 3D space with different radius. To compute a $k$-simplex, we leverage the computation performed in the round of $(k-1)$-simplices such that we can reduce the number of potential candidates to verify to improve the efficiency. An efficient verification method is proposed to confirm if a $k$-simplex can be constructed on the basis of the $(k-1)$-simplices. We demonstrate the performance with a comparison to some closely related algorithms.

翻译：在本文中, 我们提出了一个算法, 计算通用\ v{C}C}ech 复合体的有限磁盘, 每个磁盘在 2D 空间中可能有不同的半径。 这个算法的延伸也是为了在 3D 空间的一组球和不同半径。 为了计算一个 $k$- spillex, 我们利用在 $( k-1)- implices 回合中进行的计算, 这样我们就可以减少潜在候选人的数量, 以提高效率 。 提议一种有效的验证方法来确认 $k$- simpex 是否能够在 $( k-1) $- implicles 的基础上构建。 我们用与一些密切相关的算法进行比较来展示其性能 。