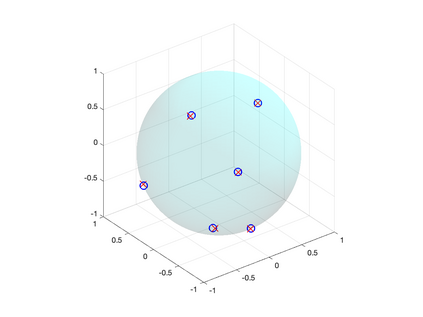
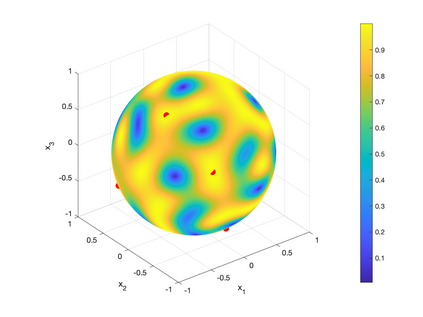
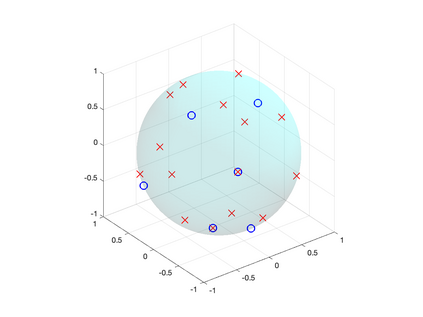
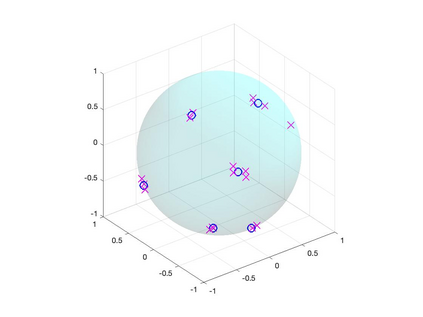
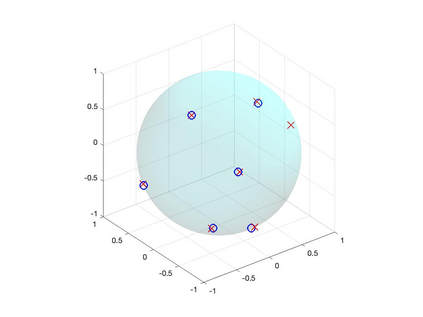
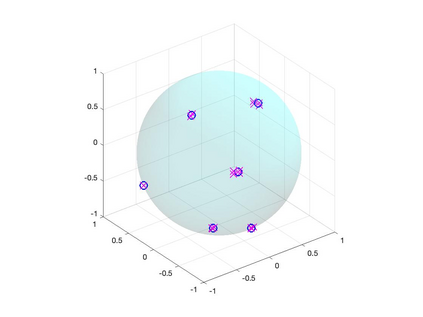
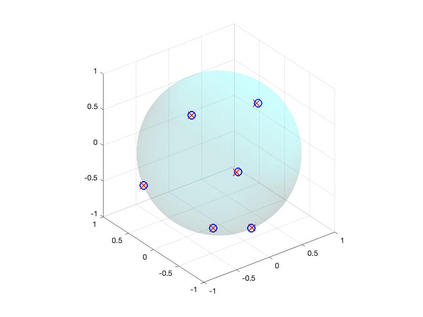
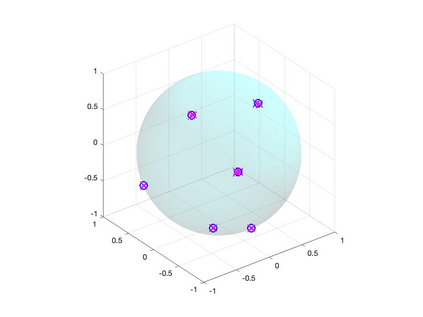
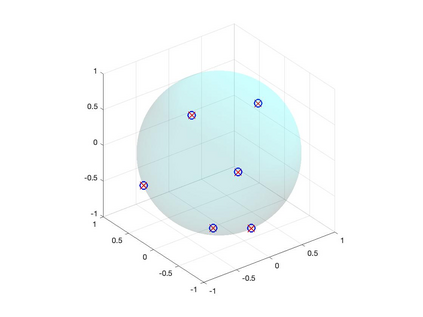
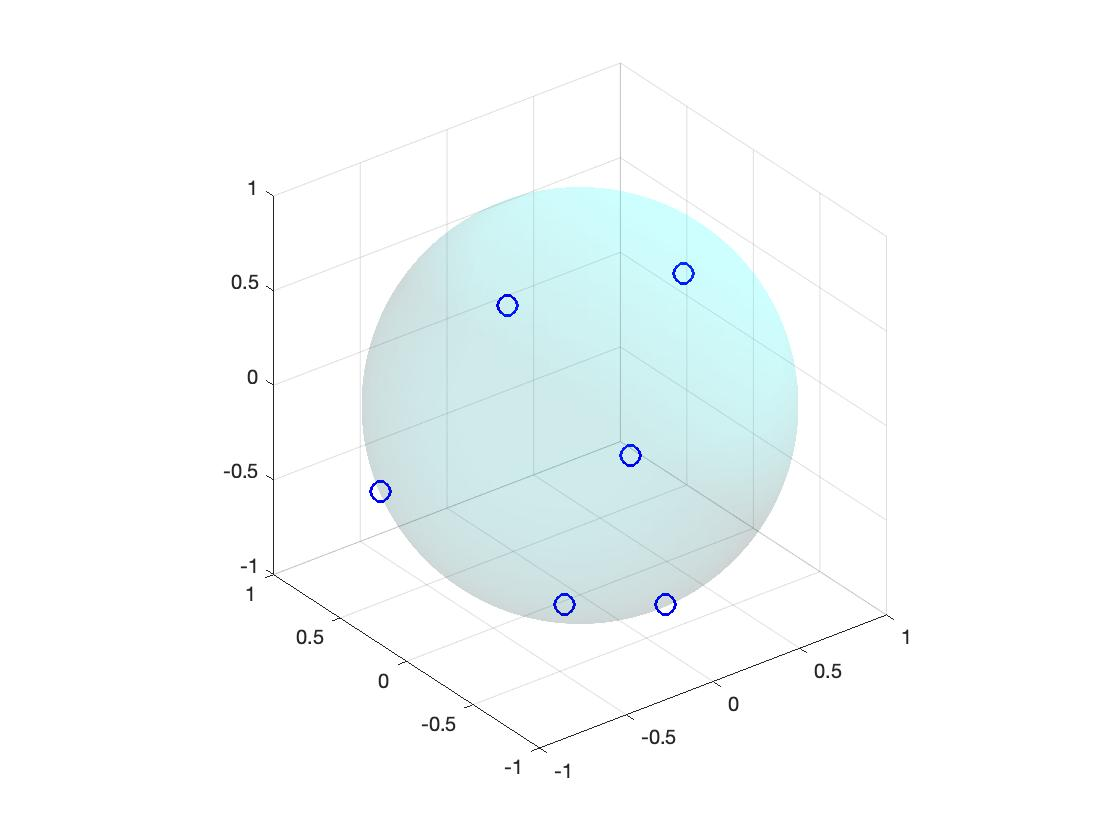
We study the problem of recovering an atomic measure on the unit 2-sphere $\mathbb{S}^2$ given finitely many moments with respect to spherical harmonics. The analysis relies on the formulation of this problem as an optimization problem on the space of bounded Borel measures on $\mathbb{S}^2$ as it was considered by Y. de Castro & F. Gamboa and E. Cand\'es & C. Fernandez-Granda. We construct a dual certificate using a kernel given in an explicit form and make a concrete analysis of the interpolation problem. Numerical examples are provided and analyzed.
翻译:我们研究了在球体口音方面有限的许多时刻恢复单元2-孔径$mathbb{S ⁇ 2$的原子测量的问题,分析依据这一问题的提法,将这一问题作为在Y. de Castro & F. Gamboa和E. Cand\es & C. Fernandez-Granda所考虑的以$mathbb{S ⁇ 2$为界限的波雷尔测量空间上的一个优化问题,我们用以明确形式提供的内核来构建双重验证,并对内插问题进行具体分析,并提供和分析数字实例。