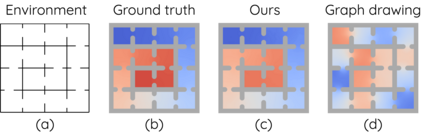
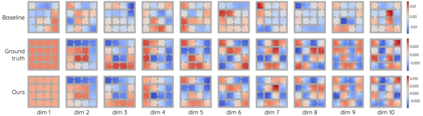
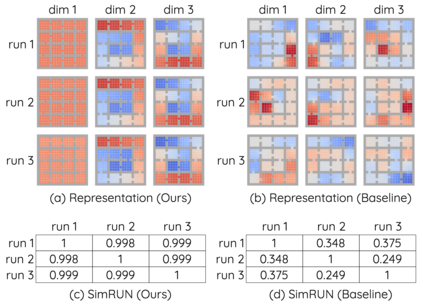
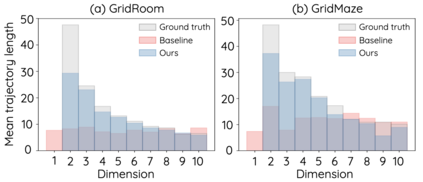
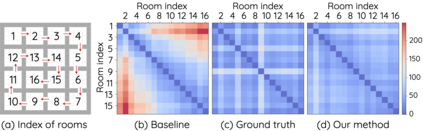
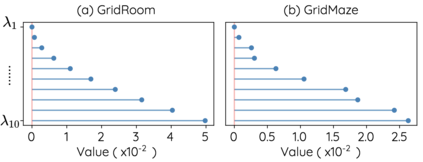
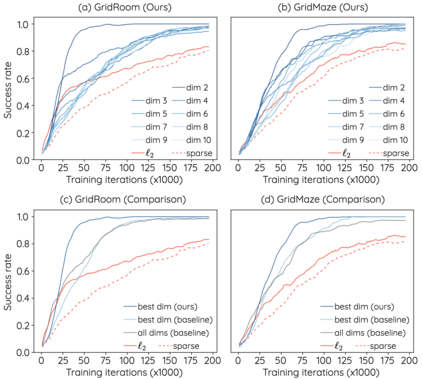
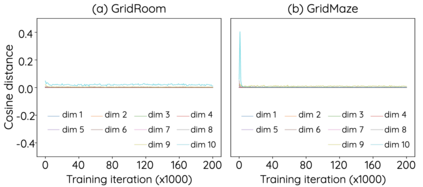
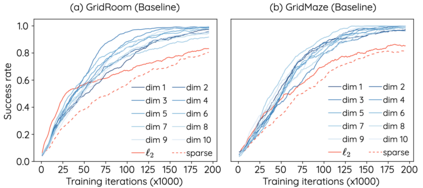
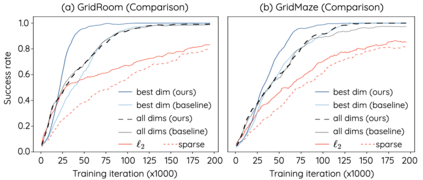
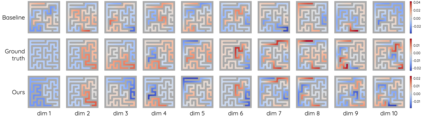
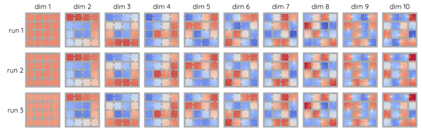
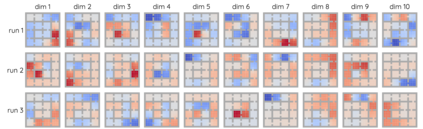
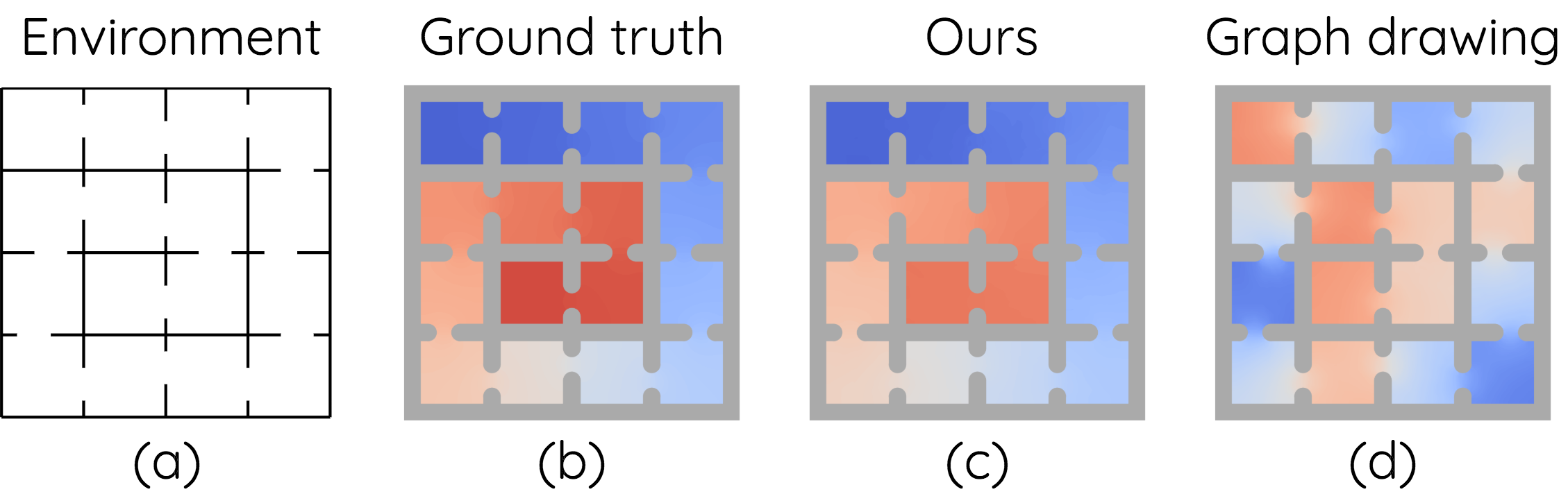
The Laplacian representation recently gains increasing attention for reinforcement learning as it provides succinct and informative representation for states, by taking the eigenvectors of the Laplacian matrix of the state-transition graph as state embeddings. Such representation captures the geometry of the underlying state space and is beneficial to RL tasks such as option discovery and reward shaping. To approximate the Laplacian representation in large (or even continuous) state spaces, recent works propose to minimize a spectral graph drawing objective, which however has infinitely many global minimizers other than the eigenvectors. As a result, their learned Laplacian representation may differ from the ground truth. To solve this problem, we reformulate the graph drawing objective into a generalized form and derive a new learning objective, which is proved to have eigenvectors as its unique global minimizer. It enables learning high-quality Laplacian representations that faithfully approximate the ground truth. We validate this via comprehensive experiments on a set of gridworld and continuous control environments. Moreover, we show that our learned Laplacian representations lead to more exploratory options and better reward shaping.

翻译：拉普拉西亚代表机构最近越来越关注强化学习,因为它为各国提供了简洁和内容翔实的代表机构,通过将国家-过渡图的拉普拉西亚矩阵作为国家嵌入体,使加强学习受到越来越多的关注。这种代表机构捕捉了基础国家空间的几何,有益于区域定位工作,例如选项发现和奖赏塑造等任务。为了在大型(甚至连续的)州空间接近拉普拉西亚代表机构,最近的工作提议尽量减少光谱图绘制目标,但这个目标除了国家衍生者之外,还有无数全球最小化机构。结果,他们学到的拉普拉西亚代表机构可能与地面真相不同。为了解决这一问题,我们重新塑造了该图表的目标,并提出了一个新的学习目标,实践证明该目标有作为独特的全球最小化机构。它能够学习忠实接近地面真相的高质量拉普拉卡西亚代表机构。我们通过对一组电网世界和连续控制环境的全面实验来验证这一点。此外,我们显示,我们所学过的拉普拉西亚代表机构代表机构代表机构能够有更多的探索性选择和更好的奖赏。