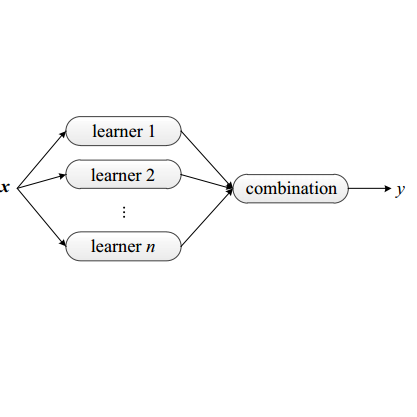
Predictions in the form of probability distributions are crucial for decision-making. Quantile regression enables this within spatial interpolation settings for merging remote sensing and gauge precipitation data. However, ensemble learning of quantile regression algorithms remains unexplored in this context. Here, we address this gap by introducing nine quantile-based ensemble learners and applying them to large precipitation datasets. We employed a novel feature engineering strategy, reducing predictors to distance-weighted satellite precipitation at relevant locations, combined with location elevation. Our ensemble learners include six stacking and three simple methods (mean, median, best combiner), combining six individual algorithms: quantile regression (QR), quantile regression forests (QRF), generalized random forests (GRF), gradient boosting machines (GBM), light gradient boosting machines (LightGBM), and quantile regression neural networks (QRNN). These algorithms serve as both base learners and combiners within different stacking methods. We evaluated performance against QR using quantile scoring functions in a large dataset comprising 15 years of monthly gauge-measured and satellite precipitation in contiguous US (CONUS). Stacking with QR and QRNN yielded the best results across quantile levels of interest (0.025, 0.050, 0.075, 0.100, 0.200, 0.300, 0.400, 0.500, 0.600, 0.700, 0.800, 0.900, 0.925, 0.950, 0.975), surpassing the reference method by 3.91% to 8.95%. This demonstrates the potential of stacking to improve probabilistic predictions in spatial interpolation and beyond.

翻译：暂无翻译