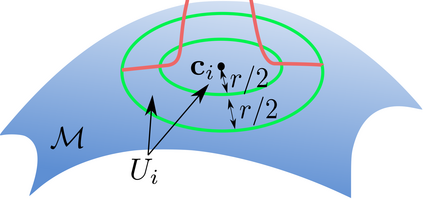
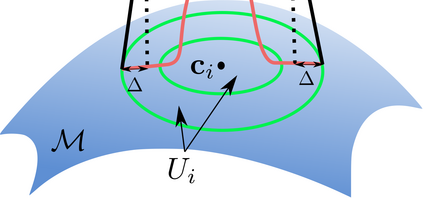
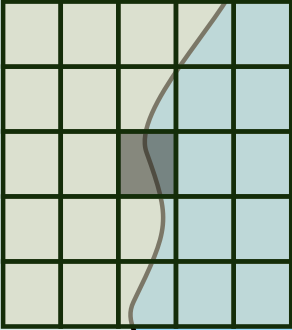
Overparameterized neural networks enjoy great representation power on complex data, and more importantly yield sufficiently smooth output, which is crucial to their generalization and robustness. Most existing function approximation theories suggest that with sufficiently many parameters, neural networks can well approximate certain classes of functions in terms of the function value. The neural network themselves, however, can be highly nonsmooth. To bridge this gap, we take convolutional residual networks (ConvResNets) as an example, and prove that large ConvResNets can not only approximate a target function in terms of function value, but also exhibit sufficient first-order smoothness. Moreover, we extend our theory to approximating functions supported on a low-dimensional manifold. Our theory partially justifies the benefits of using deep and wide networks in practice. Numerical experiments on adversarial robust image classification are provided to support our theory.

翻译：超临界神经网络在复杂数据上拥有巨大的代表力,更重要的是,它能产生足够平稳的输出,这对于其一般化和稳健性至关重要。 多数现有功能近似理论表明,如果参数足够多,神经网络就能够从功能值方面大致接近某些功能类别。 但是,神经网络本身可能高度不失色。为了缩小这一差距,我们以变速残余网络(ConvResNets)为例,并证明大型ConvResNet不仅能够从功能值方面接近目标功能,而且能够表现出足够的第一阶平稳性。此外,我们把理论推广到以低维维维维维支持的类似功能上。我们的理论部分地证明在实践中使用深宽网络的好处是有道理的。 为支持我们的理论,提供了关于对抗性强势图像分类的数值实验。