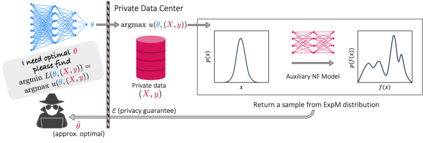
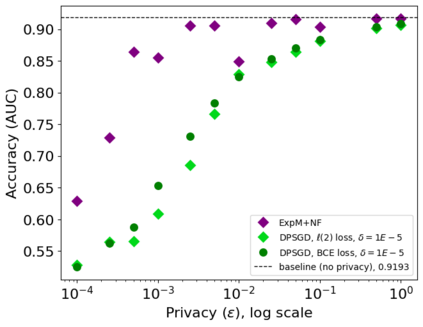
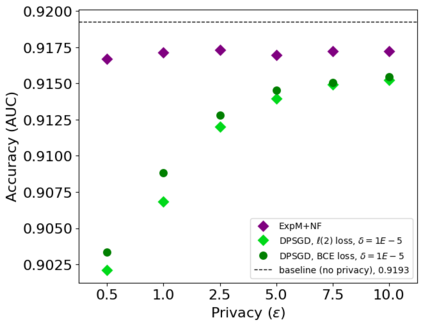
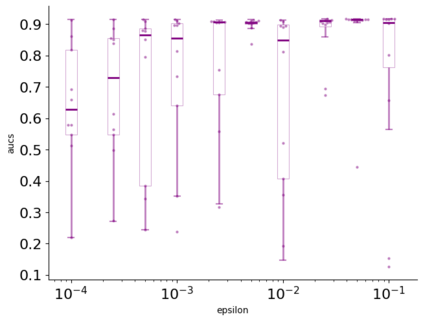
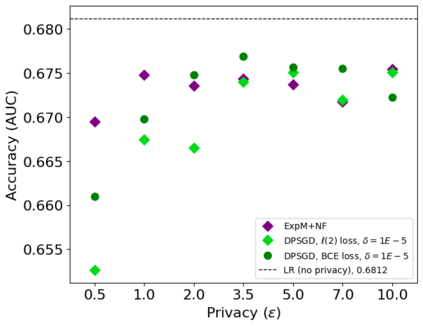
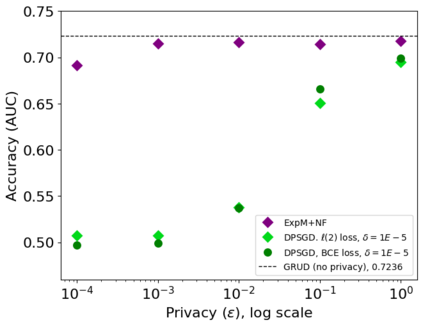
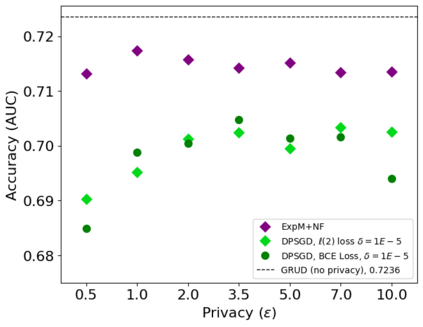
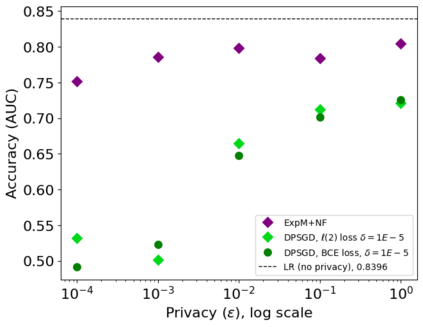
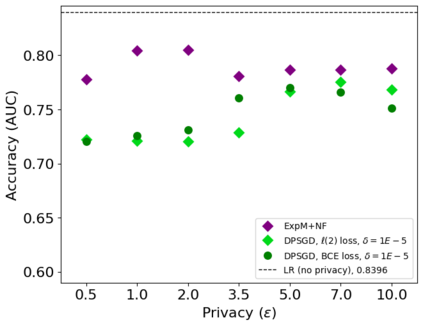
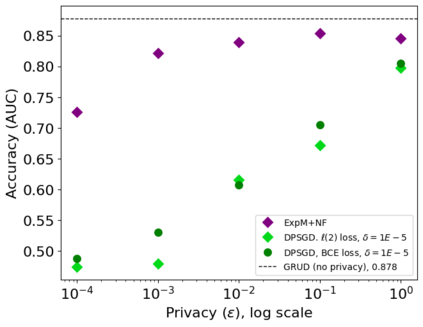
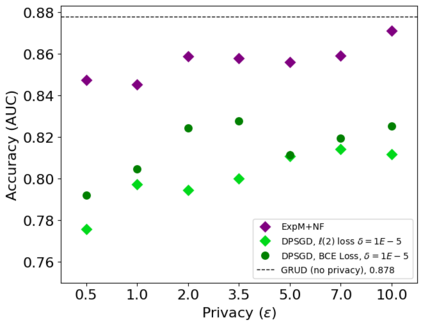
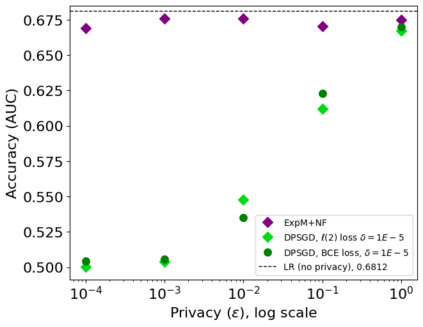
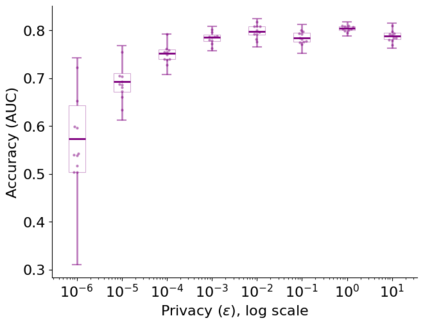
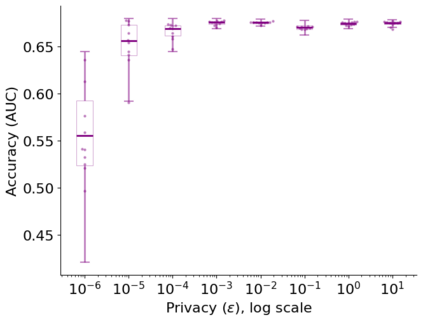
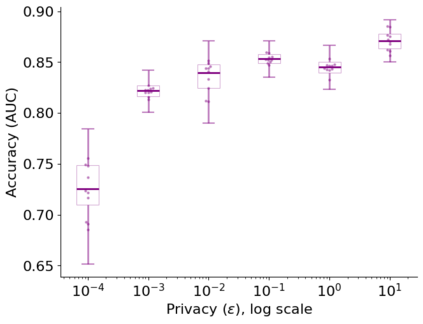
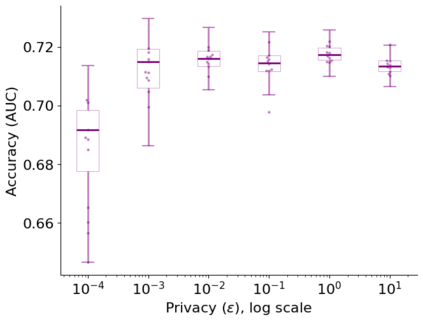
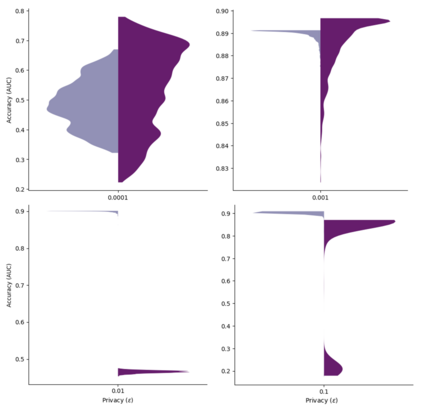
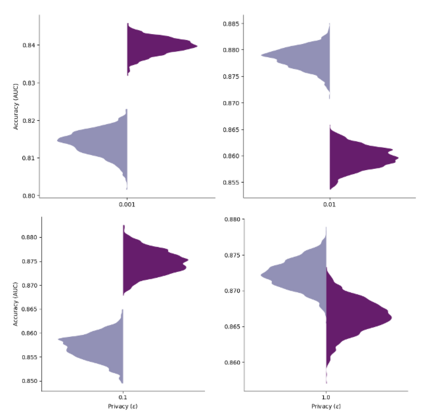
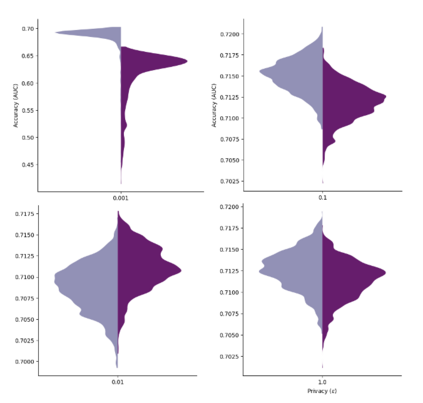
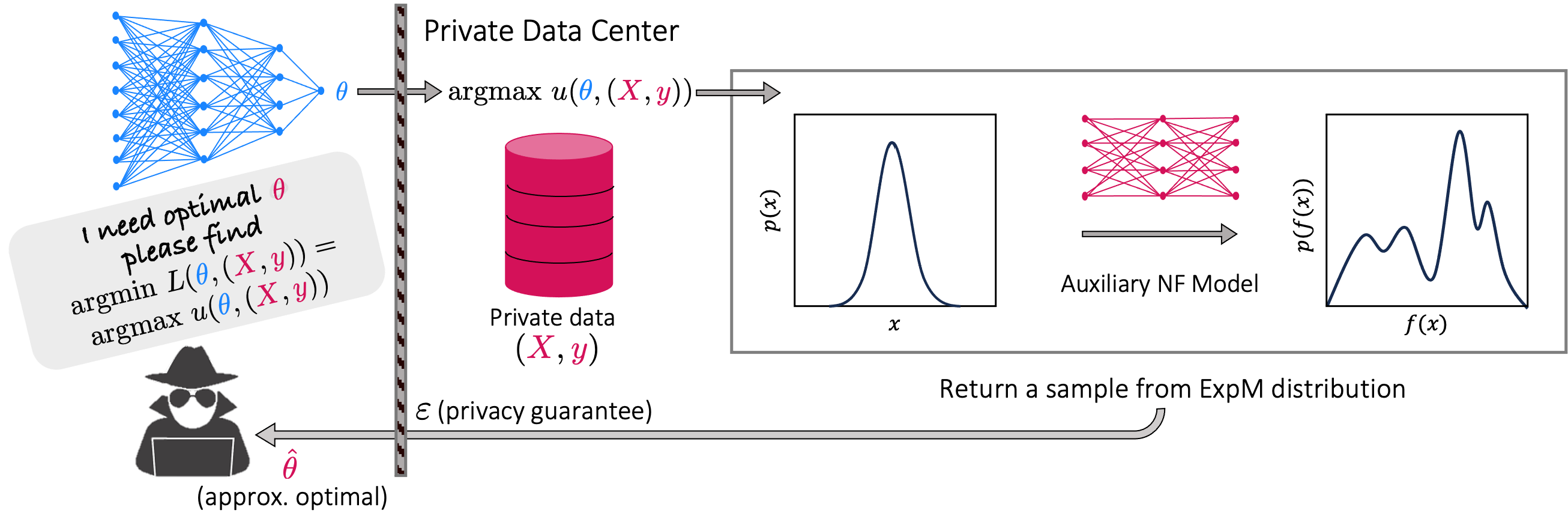
In this pioneering work we formulate ExpM+NF, a method for training machine learning (ML) on private data with pre-specified differentially privacy guarantee $\varepsilon>0, \delta=0$, by using the Exponential Mechanism (ExpM) and an auxiliary Normalizing Flow (NF). We articulate theoretical benefits of ExpM+NF over Differentially Private Stochastic Gradient Descent (DPSGD), the state-of-the-art (SOTA) and de facto method for differentially private ML, and we empirically test ExpM+NF against DPSGD using the SOTA implementation (Opacus with PRV accounting) in multiple classification tasks on the Adult Dataset (census data) and MIMIC-III Dataset (electronic healthcare records) using Logistic Regression and GRU-D, a deep learning recurrent neural network with ~20K-100K parameters. In all experiments, ExpM+NF achieves greater than 93% of the non-private training accuracy (AUC) for $\varepsilon \in [1\mathrm{e}{-3}, 1]$, exhibiting greater accuracy (higher AUC) and privacy (lower $\varepsilon$ with $\delta=0$) than DPSGD. Differentially private ML generally considers $\varepsilon \in [1,10]$ to maintain reasonable accuracy; hence, ExpM+NF's ability to provide strong accuracy for orders of magnitude better privacy (smaller $\varepsilon$) substantially pushes what is currently possible in differentially private ML. Training time results are presented showing ExpM+NF is comparable to (slightly faster) than DPSGD. Code for these experiments will be provided after review. Limitations and future directions are provided.

翻译：暂无翻译