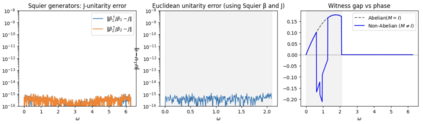
We introduce a frequency-tunable, two-dimensional non-Abelian control of operation order constructed from the reduced Burau representation of the braid group $B_3$, specialised at $t=e^{i\omega}$ and unitarized by Squier's Hermitian form. Coupled to two non-commuting qubit unitaries $A,B$, the resulting switch admits a closed expression for the single-shot Helstrom success probability and a fixed-order ceiling $p_{\mathrm{fixed}}$, defining the analytic witness gap $\Delta(\omega)=p_{\mathrm{switch}}(\omega)-p_{\mathrm{fixed}}$. The sign change of $\Delta(\omega)$ across the Squier positivity window reveals alternating constructive and destructive interference of causal orders, a hallmark of non-Abelian control, while $\Delta(\omega)>0$ certifies algebraic causal non-separability. Numerical simulations confirm both enhancement and suppression regimes, establishing a minimal $B_3$ braid control that reproduces the characteristic interference pattern expected from a Gedankenexperiment in anyonic statistics.

翻译：暂无翻译