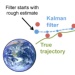
Advances in tracking technologies for animal movement require new statistical tools to better exploit the increasing amount of data. Animal positions are usually calculated using the GPS or Argos satellite system and include potentially complex non-Gaussian and heavy-tailed measurement error patterns. Errors are usually handled through a Kalman filter algorithm, which can be sensitive to non-Gaussian error distributions. In this paper, we introduce a realistic latent movement model through an underdamped Langevin stochastic differential equation (SDE) that includes an additional drift term to ensure that the animal remains in a known spatial domain of interest. This can be applied to aquatic animals moving in water or terrestrial animals moving in a restricted zone delimited by fences or natural barriers. We demonstrate that the incorporation of these spatial constraints into the latent movement model improves the accuracy of filtering for noisy observations of the positions. We implement an Extended Kalman Filter as well as a particle filter adapted to non-Gaussian error distributions. Our filters are based on solving the SDE through splitting schemes to approximate the latent dynamic.

翻译：暂无翻译