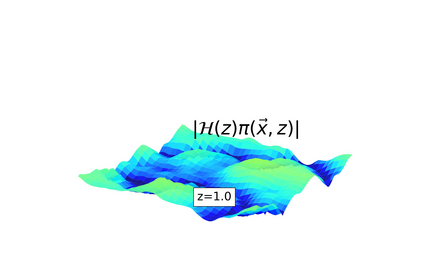
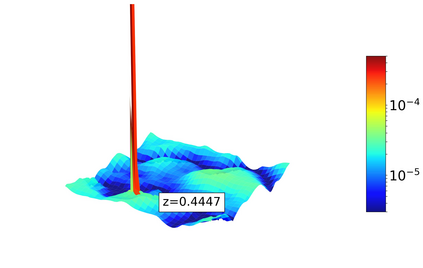
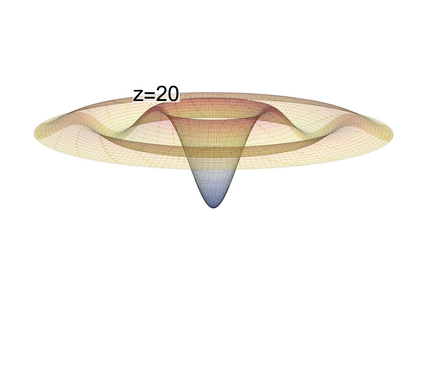
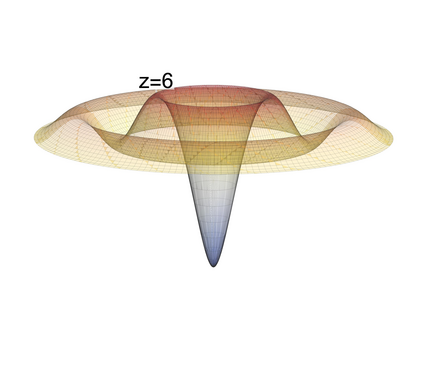
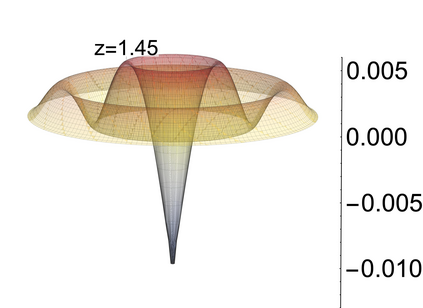
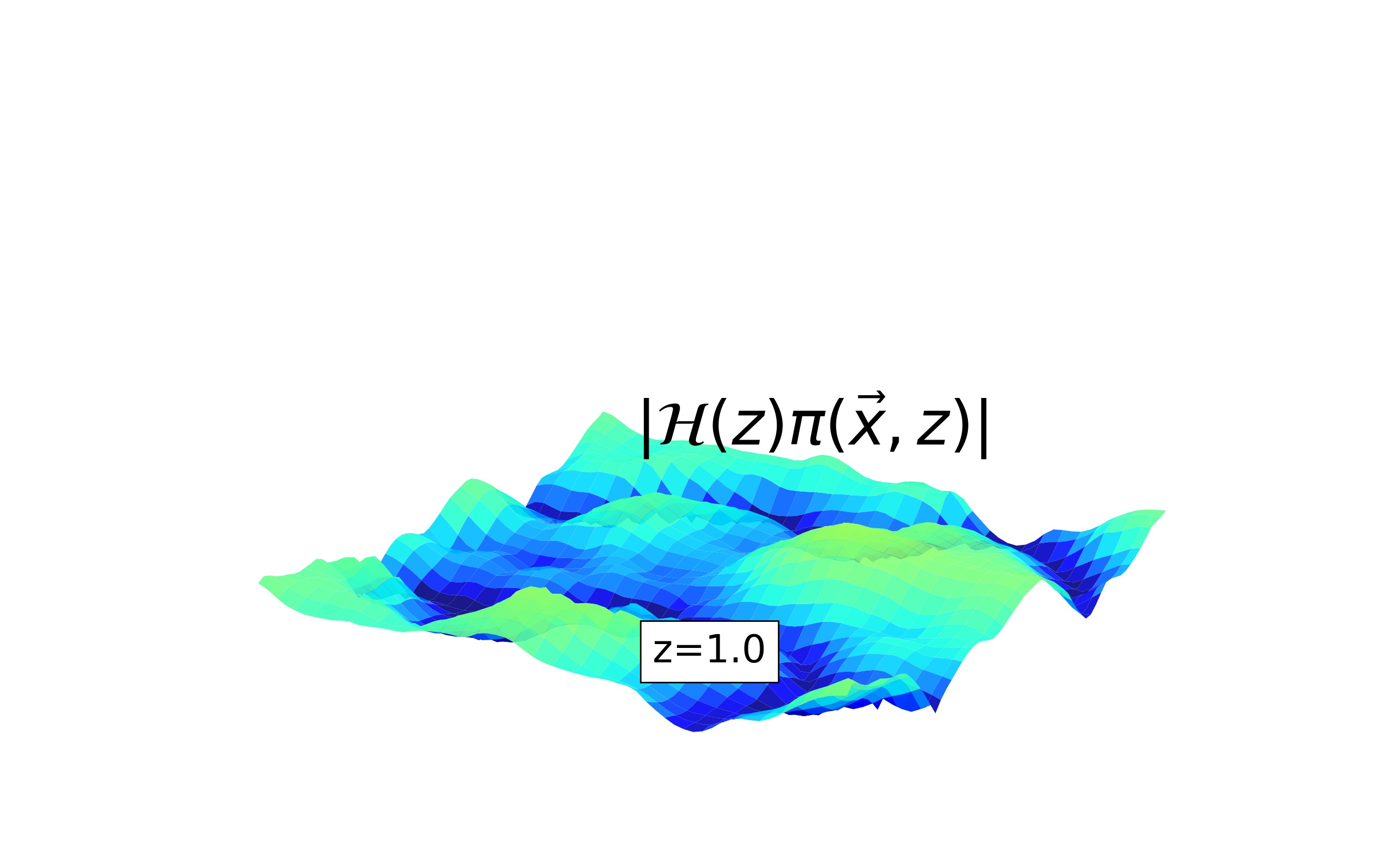
In this letter we introduce the non-linear partial differential equation (PDE) $\partial^2_{\tau} \pi \propto (\vec\nabla \pi)^2$ showing a new type of instability. Such equations appear in the effective field theory (EFT) of dark energy for the $k$-essence model as well as in many other theories based on the EFT formalism. We demonstrate the occurrence of instability in the cosmological context using a relativistic $N$-body code, and we study it mathematically in 3+1 dimensions within spherical symmetry. We show that this term dominates for the low speed of sound limit where some important linear terms are suppressed.

翻译：在这封信中,我们引入了非线性部分偏差方程( PDE) $\ part=2\\\\\ tau}\ pi\ propto (\vec\nabla\ pi)\\ $2$ 显示一种新的不稳定性。这种方程出现在$k$- essence 模型的有效暗能量领域理论( EFT) 以及基于 EFT 形式主义的许多其他理论中。 我们用相对论的 $N$- body 代码来证明宇宙环境中的不稳定,我们用数学方法在球体对称范围内的3+1 维上进行了研究。 我们显示,该术语在抑制一些重要线性术语的低音速限制中占主导地位。