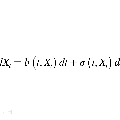Objective: To validate a newly proposed stochastic differential equation (SDE)-based model for proton beam energy deposition by comparing its predictions with those from Geant4 in simplified phantom scenarios. Approach: Building on previous work in Crossley et al. (2025), where energy deposition from a proton beam was modelled using an SDE framework, we implemented the model with standard approximations to interaction cross sections and mean excitation energies, which makes simulations easily adaptable to new materials and configurations. The model was benchmarked against Geant4 in homogeneous and heterogeneous phantoms. Main results: The SDE-based dose distributions agreed well with Geant4, showing range differences within 0.4 mm and 3D gamma pass rates exceeding 98% under 3%/2 mm criteria with a 1% dose threshold. The model achieved a computational speed-up of approximately fivefold relative to Geant4, consistent across different Geant4 physics lists. Significance: These results demonstrate that the SDE approach can reproduce accuracy comparable to high-fidelity Monte Carlo for proton therapy at a fraction of the computational cost, highlighting its potential for accelerating dose calculations and treatment planning.
翻译:目的:通过将新提出的基于随机微分方程(SDE)的质子束能量沉积模型的预测结果与Geant4在简化模体场景下的结果进行比较,以验证该模型的有效性。方法:基于Crossley等人(2025)先前将质子束能量沉积建模为SDE框架的研究,我们采用相互作用截面和平均激发能的标准近似实现了该模型,这使得模拟能够轻松适应新材料和配置。该模型在均匀和非均匀模体中对Geant4进行了基准测试。主要结果:基于SDE的剂量分布与Geant4结果吻合良好,射程差异在0.4毫米以内,在3%/2毫米标准及1%剂量阈值下,三维伽马通过率超过98%。该模型相对于Geant4实现了约五倍的计算加速,且在不同Geant4物理列表下表现一致。意义:这些结果表明,SDE方法能够以较低的计算成本复现与高保真蒙特卡罗方法相当的质子治疗精度,突显了其在加速剂量计算和治疗计划方面的潜力。