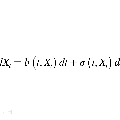Backward stochastic differential equation (BSDE)-based deep learning methods provide an alternative to Physics-Informed Neural Networks (PINNs) for solving high-dimensional partial differential equations (PDEs), offering potential algorithmic advantages in settings such as stochastic optimal control, where the PDEs of interest are tied to an underlying dynamical system. However, standard BSDE-based solvers have empirically been shown to underperform relative to PINNs in the literature. In this paper, we identify the root cause of this performance gap as a discretization bias introduced by the standard Euler-Maruyama (EM) integration scheme applied to one-step self-consistency BSDE losses, which shifts the optimization landscape off target. We find that this bias cannot be satisfactorily addressed through finer step-sizes or multi-step self-consistency losses. To properly handle this issue, we propose a Stratonovich-based BSDE formulation, which we implement with stochastic Heun integration. We show that our proposed approach completely eliminates the bias issues faced by EM integration. Furthermore, our empirical results show that our Heun-based BSDE method consistently outperforms EM-based variants and achieves competitive results with PINNs across multiple high-dimensional benchmarks. Our findings highlight the critical role of integration schemes in BSDE-based PDE solvers, an algorithmic detail that has received little attention thus far in the literature.

翻译：基于倒向随机微分方程（BSDE）的深度学习方法为求解高维偏微分方程（PDE）提供了物理信息神经网络（PINNs）之外的替代方案，在随机最优控制等场景中具有潜在算法优势，因为此类PDE与底层动态系统紧密关联。然而，现有文献表明标准BSDE求解器在实证中表现通常逊于PINNs。本文指出，性能差距的根本原因在于标准欧拉-丸山（EM）积分方案应用于单步自洽BSDE损失时引入的离散化偏差，该偏差使优化目标发生偏移。研究发现，通过更细时间步长或多步自洽损失均无法有效解决此偏差问题。为此，我们提出基于Stratonovich积分的BSDE表述框架，并采用随机Heun积分法实现。理论证明该方法完全消除了EM积分面临的偏差问题。实证结果表明，基于Heun积分的BSDE方法在多个高维基准测试中持续优于EM变体，并与PINNs取得可比性能。本研究揭示了积分方案在BSDE类PDE求解器中的关键作用，这一算法细节在当前文献中尚未得到充分关注。