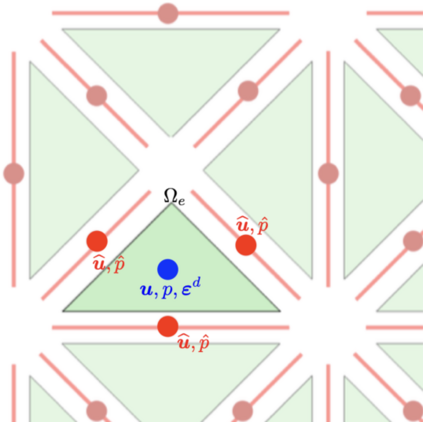
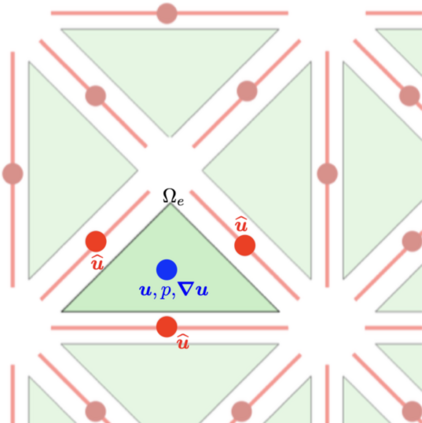
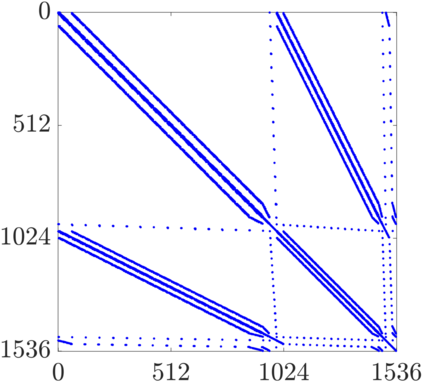
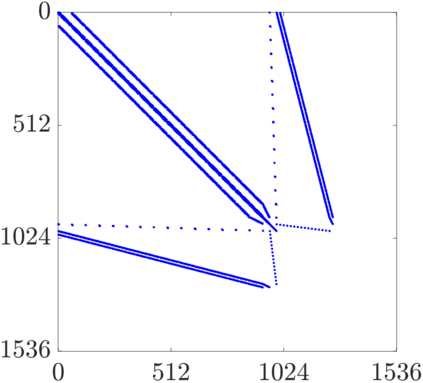
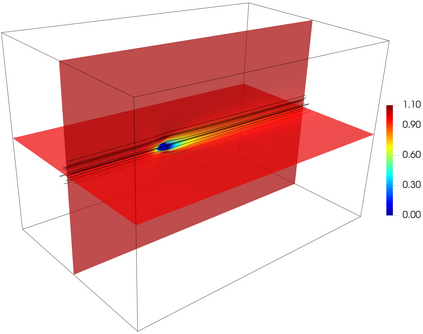
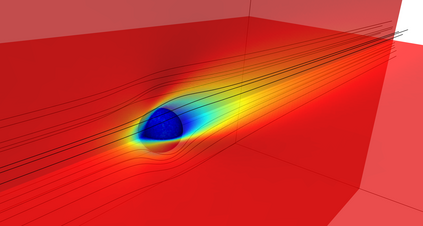
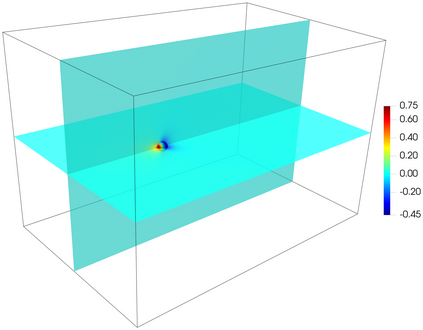
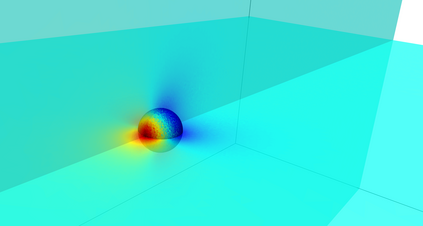
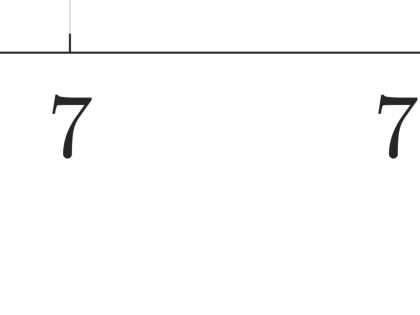
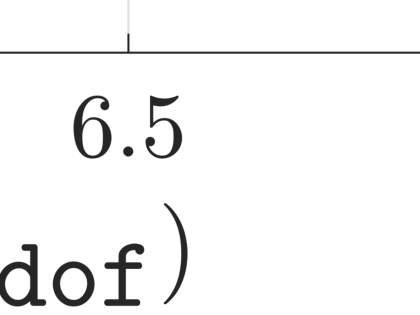This work presents a hybrid pressure face-centred finite volume (FCFV) solver to simulate steady-state incompressible Navier-Stokes flows. The method leverages the robustness, in the incompressible limit, of the hybridisable discontinuous Galerkin paradigm for compressible and weakly compressible flows to derive the formulation of a novel, low-order face-based discretisation. The incompressibility constraint is enforced in a weak sense, by introducing an inter-cell mass flux defined in terms of a new, hybrid variable, representing the pressure at the cell faces. This results in a new hybridisation strategy where cell variables (velocity, pressure and deviatoric strain rate tensor) are expressed as a function of velocity and pressure at the barycentre of the cell faces. The hybrid pressure formulation provides first-order convergence of all variables, including the stress, without the need for gradient reconstruction, thus being less sensitive to cell type, stretching, distortion, and skewness than traditional low-order finite volume solvers. Numerical benchmarks of Navier-Stokes flows at low and moderate Reynolds numbers, in two and three dimensions, are presented to evaluate accuracy and robustness of the method. In particular, the hybrid pressure formulation outperforms the FCFV method when convective effects are relevant, achieving accurate predictions on significantly coarser meshes.

翻译：暂无翻译