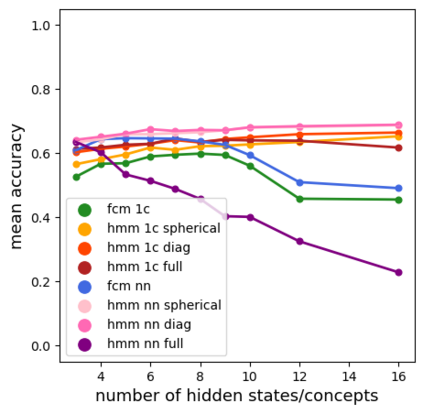
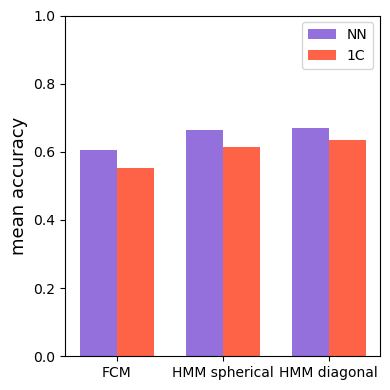
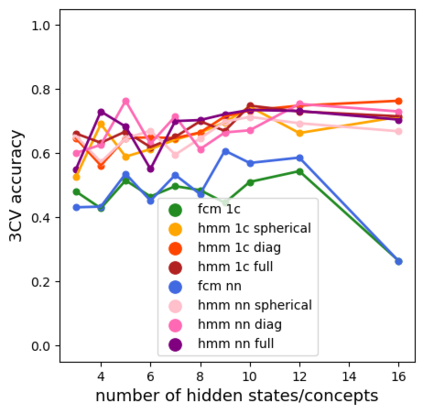
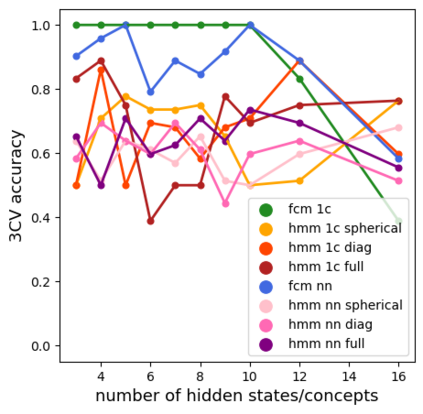
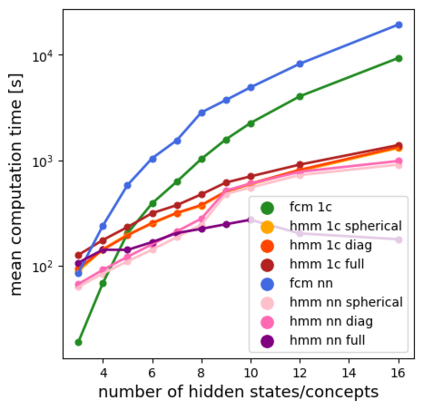
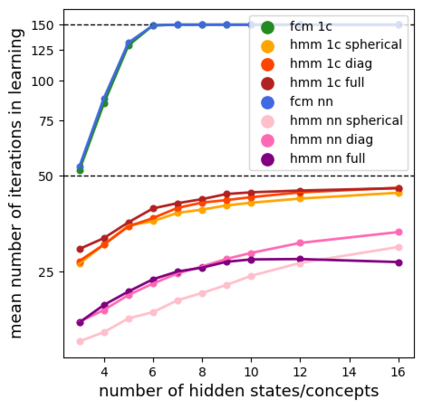
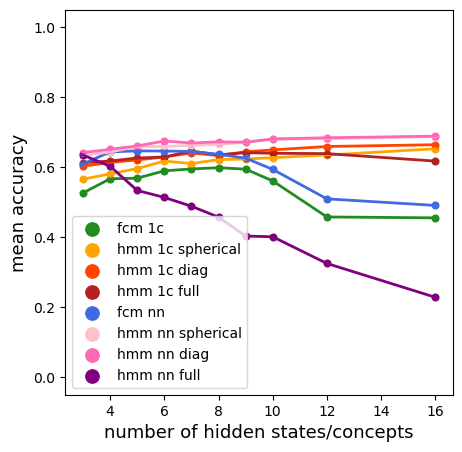
Time series classification is one of the very popular machine learning tasks. In this paper, we explore the application of Hidden Markov Model (HMM) for time series classification. We distinguish between two modes of HMM application. The first, in which a single model is built for each class. The second, in which one HMM is built for each time series. We then transfer both approaches for classifier construction to the domain of Fuzzy Cognitive Maps. The identified four models, HMM NN (HMM, one per series), HMM 1C (HMM, one per class), FCM NN, and FCM 1C are then studied in a series of experiments. We compare the performance of different models and investigate the impact of their hyperparameters on the time series classification accuracy. The empirical evaluation shows a clear advantage of the one-model-per-series approach. The results show that the choice between HMM and FCM should be dataset-dependent.

翻译：时间序列分类是十分流行的机器学习任务之一。 在本文中, 我们探索了隐性马尔科夫模型( HMM) 用于时间序列分类的应用。 我们区分了两种HMM应用模式。 首先, 为每类设计了一个单一模型; 第二, 为每时间序列设计了一个 HMM 。 然后, 我们将两种分类构建方法转移到 Fuzzy Cognitive Maps 领域。 确定的四种模式, HMMN (HMM, 每系列一个)、 HMM 1C (HMM, 每类一个)、 FCM NN 和 FCM 1C 进行一系列实验研究。 我们比较了不同模型的性能, 并调查其超参数对时间序列分类准确性的影响。 实证评估显示了单系列方法的明显优势。 结果显示, HMMM 和 FCM 之间的选择应该取决于数据设置 。