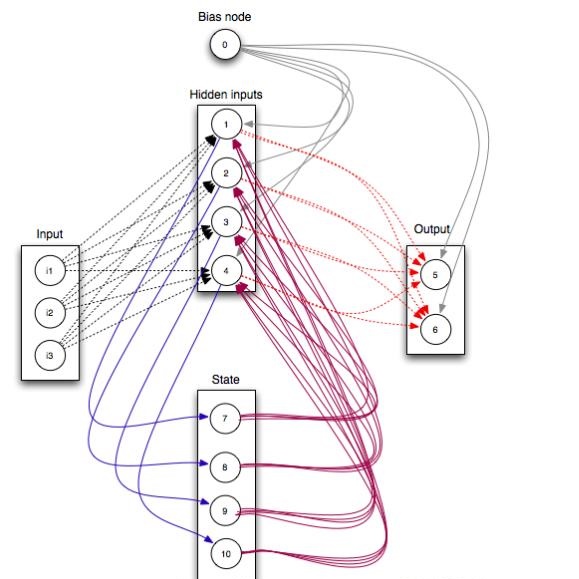
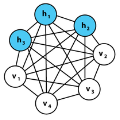
We investigate a framework for binary image denoising via restricted Boltzmann machines (RBMs) that introduces a denoising objective in quadratic unconstrained binary optimization (QUBO) form and is well-suited for quantum annealing. The denoising objective is attained by balancing the distribution learned by a trained RBM with a penalty term for derivations from the noisy image. We derive the statistically optimal choice of the penalty parameter assuming the target distribution has been well-approximated, and further suggest an empirically supported modification to make the method robust to that idealistic assumption. We also show under additional assumptions that the denoised images attained by our method are, in expectation, strictly closer to the noise-free images than the noisy images are. While we frame the model as an image denoising model, it can be applied to any binary data. As the QUBO formulation is well-suited for implementation on quantum annealers, we test the model on a D-Wave Advantage machine, and also test on data too large for current quantum annealers by approximating QUBO solutions through classical heuristics.

翻译：暂无翻译