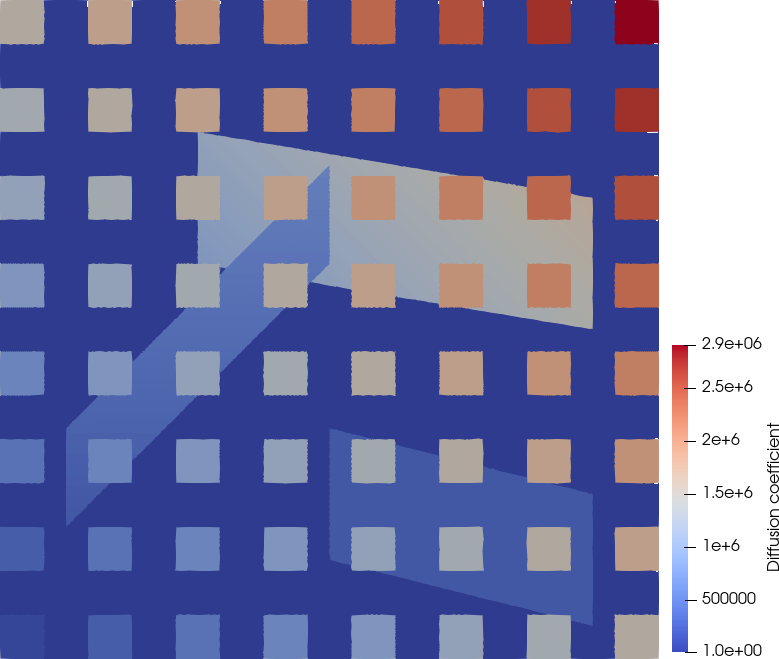
Coarse spaces are essential to ensure robustness w.r.t. the number of subdomains in two-level overlapping Schwarz methods. Robustness with respect to the coefficients of the underlying partial differential equation (PDE) can be achieved by adaptive (or spectral) coarse spaces involving the solution of local eigenproblems. The solution of these eigenproblems, although scalable, entails a large setup cost which may exceed the cost for the iteration phase. In this paper we present and analyse a new variant of the GenEO (Generalised Eigenproblems in the Overlap) coarse space which involves solving eigenproblems only in a strip connected to the boundary of the subdomain. This leads to a significant reduction of the setup cost while the method satisfies a similar coefficient-robust condition number estimate as the original method, albeit with a possibly larger coarse space.

翻译：暂无翻译