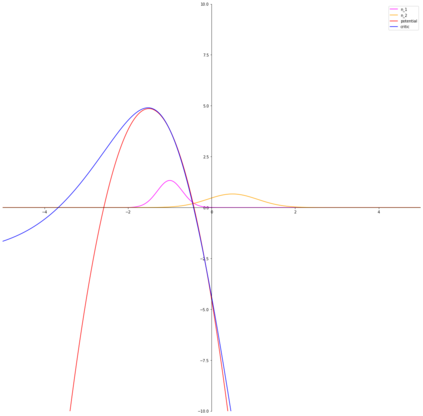
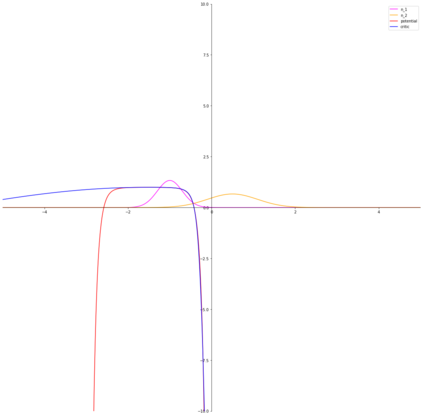
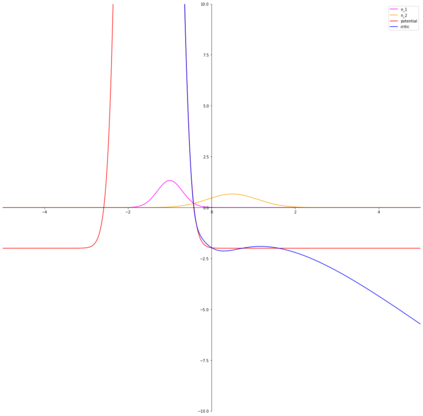
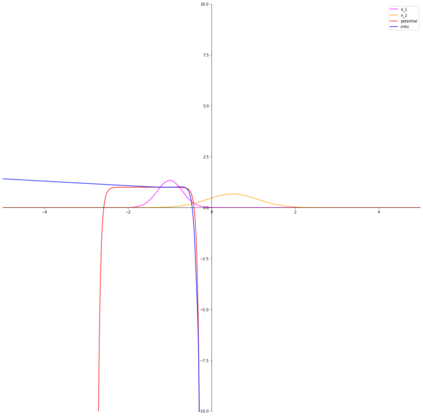
Variational representations of $f$-divergences are central to many machine learning algorithms, with Lipschitz constrained variants recently gaining attention. Inspired by this, we generalize the so-called tight variational representation of $f$-divergences in the case of probability measures on compact metric spaces to be taken over the space of Lipschitz functions vanishing at an arbitrary base point, characterize functions achieving the supremum in the variational representation, propose a practical algorithm to calculate the tight convex conjugate of $f$-divergences compatible with automatic differentiation frameworks, define the Moreau-Yosida approximation of $f$-divergences with respect to the Wasserstein-$1$ metric, and derive the corresponding variational formulas, providing a generalization of a number of recent results, novel special cases of interest and a relaxation of the hard Lipschitz constraint. As an application of our theoretical results, we propose the Moreau-Yosida $f$-GAN, providing an implementation of the variational formulas for the Kullback-Leibler, reverse Kullback-Leibler, $\chi^2$, reverse $\chi^2$, squared Hellinger, Jensen-Shannon, Jeffreys, triangular discrimination and total variation divergences as GANs trained on CIFAR-10, leading to competitive results and a simple solution to the problem of uniqueness of the optimal critic.

翻译：以美元计价的变异表示是许多机器学习算法的核心,而利普西茨受限制的变异体最近受到注意。受此启发,我们普遍采用所谓的“最紧的变异代表”即美元-调高,如果对利普西茨功能空间采取紧凑的衡量标准,在任意的基点消失时,对利普西茨功能空间采取的可能性措施,说明在变异代表制中实现超优的功能的特点,提出一个实际的算法,以计算与自动差异框架兼容的美元-调高的紧紧合,界定与瓦塞斯坦-1美元比值相比的 " Moreau-Yosida " 近似值,并得出相应的变异公式,对近期的一些结果、新的特别感兴趣案例和利普西茨基茨约束的放松。作为我们理论结果的应用,我们提议采用 " 莫罗-尤-Yosida $-GAN ",为核心-可逆、REF2、REF-C-C-CRal-C-CRal-CRal-CRial-Real-Real-Cal-Cal-Cal-Cal-Cal-Cal-Cal-Cal-Cal-Cal-Cal-Cal-Colvers可变价,对可变制价、K-CRU-CRU-CRU-CU-C-C-CU-C-C-C-CU-CU-CFM-C-CFM-C-C-C-C-C-CFM-CU-C-C-C-C-C-C-C-C-C-C-C-CU-C-C-C-C-C-C-C-C-C-C-C-C-C-CU-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-I-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C-C